Lost in the Shuffle: Testing Power in the Presence of Errorful Network Vertex Labels

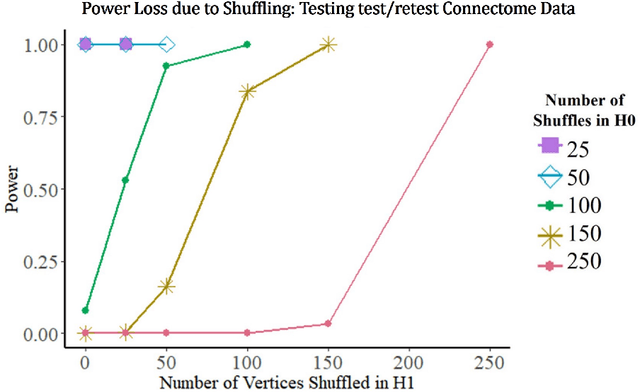
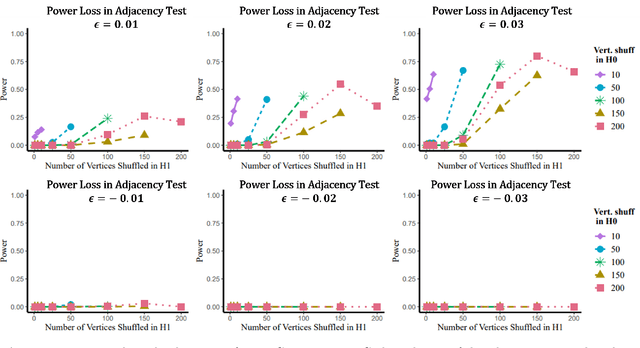
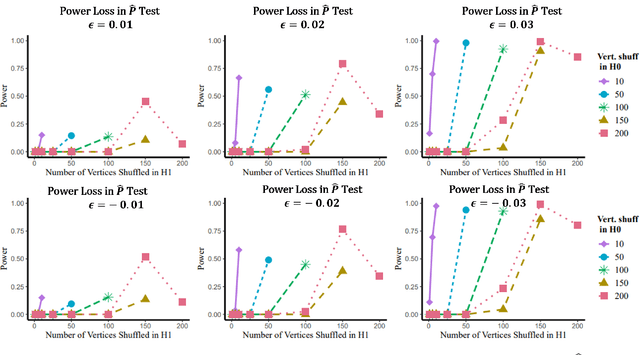
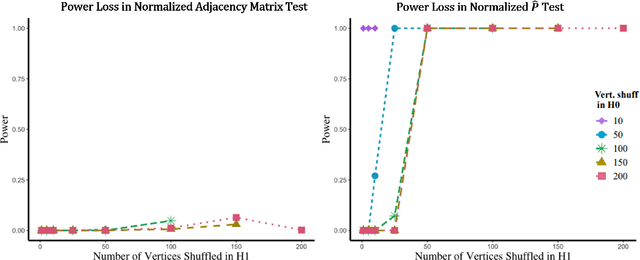
Many two-sample network hypothesis testing methodologies operate under the implicit assumption that the vertex correspondence across networks is a priori known. In this paper, we consider the degradation of power in two-sample graph hypothesis testing when there are misaligned/label-shuffled vertices across networks. In the context of stochastic block model networks, we theoretically explore the power loss due to shuffling for a pair of hypothesis tests based on Frobenius norm differences between estimated edge probability matrices or between adjacency matrices. The loss in testing power is further reinforced by numerous simulations and experiments, both in the stochastic block model and in the random dot product graph model, where we compare the power loss across multiple recently proposed tests in the literature. Lastly, we demonstrate the impact that shuffling can have in real-data testing in a pair of examples from neuroscience and from social network analysis.