Learning the effect of latent variables in Gaussian Graphical models with unobserved variables
Paper and Code
Jul 31, 2018
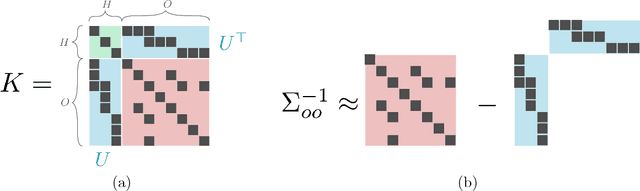
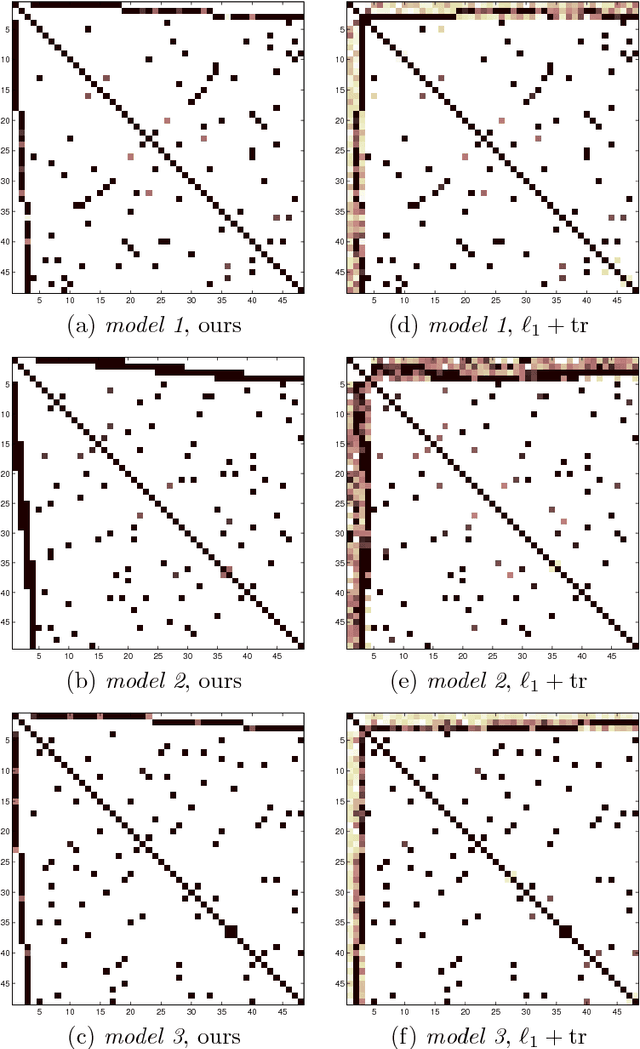
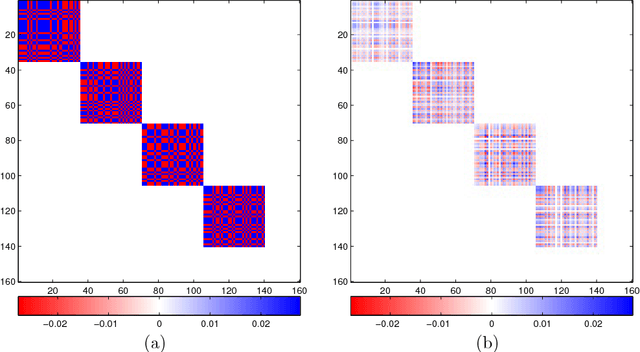
The edge structure of the graph defining an undirected graphical model describes precisely the structure of dependence between the variables in the graph. In many applications, the dependence structure is unknown and it is desirable to learn it from data, often because it is a preliminary step to be able to ascertain causal effects. This problem, known as structure learning, is hard in general, but for Gaussian graphical models it is slightly easier because the structure of the graph is given by the sparsity pattern of the precision matrix of the joint distribution, and because independence coincides with decorrelation. A major difficulty too often ignored in structure learning is the fact that if some variables are not observed, the marginal dependence graph over the observed variables will possibly be significantly more complex and no longer reflect the direct dependencies that are potentially associated with causal effects. In this work, we consider a family of latent variable Gaussian graphical models in which the graph of the joint distribution between observed and unobserved variables is sparse, and the unobserved variables are conditionally independent given the others. Prior work was able to recover the connectivity between observed variables, but could only identify the subspace spanned by unobserved variables, whereas we propose a convex optimization formulation based on structured matrix sparsity to estimate the complete connectivity of the complete graph including unobserved variables, given the knowledge of the number of missing variables, and a priori knowledge of their level of connectivity. Our formulation is supported by a theoretical result of identifiability of the latent dependence structure for sparse graphs in the infinite data limit. We propose an algorithm leveraging recent active set methods, which performs well in the experiments on synthetic data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge