Learning Probabilistic Logic Programs in Continuous Domains
Paper and Code
Sep 19, 2018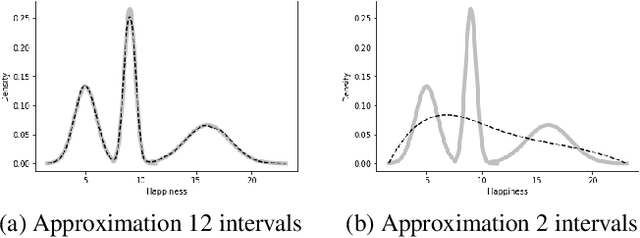
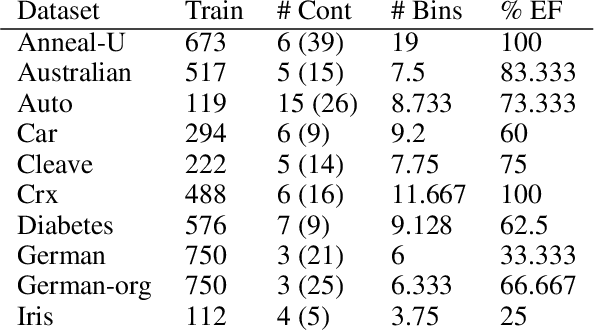
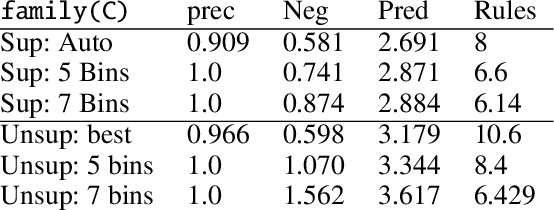
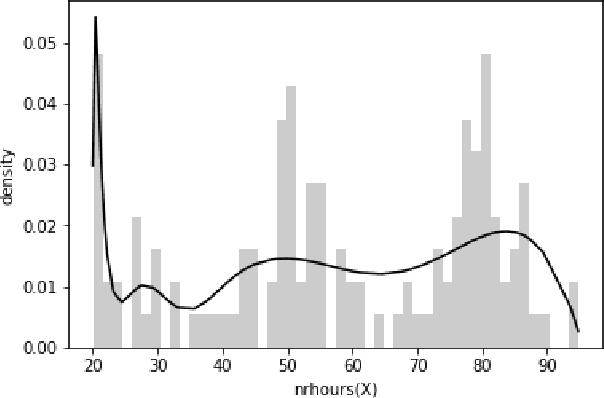
The field of statistical relational learning aims at unifying logic and probability to reason and learn from data. Perhaps the most successful paradigm in the field is probabilistic logic programming: the enabling of stochastic primitives in logic programming, which is now increasingly seen to provide a declarative background to complex machine learning applications. While many systems offer inference capabilities, the more significant challenge is that of learning meaningful and interpretable symbolic representations from data. In that regard, inductive logic programming and related techniques have paved much of the way for the last few decades. Unfortunately, a major limitation of this exciting landscape is that much of the work is limited to finite-domain discrete probability distributions. Recently, a handful of systems have been extended to represent and perform inference with continuous distributions. The problem, of course, is that classical solutions for inference are either restricted to well-known parametric families (e.g., Gaussians) or resort to sampling strategies that provide correct answers only in the limit. When it comes to learning, moreover, inducing representations remains entirely open, other than "data-fitting" solutions that force-fit points to aforementioned parametric families. In this paper, we take the first steps towards inducing probabilistic logic programs for continuous and mixed discrete-continuous data, without being pigeon-holed to a fixed set of distribution families. Our key insight is to leverage techniques from piecewise polynomial function approximation theory, yielding a principled way to learn and compositionally construct density functions. We test the framework and discuss the learned representations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge