Latent space models for multiplex networks with shared structure
Paper and Code
Dec 28, 2020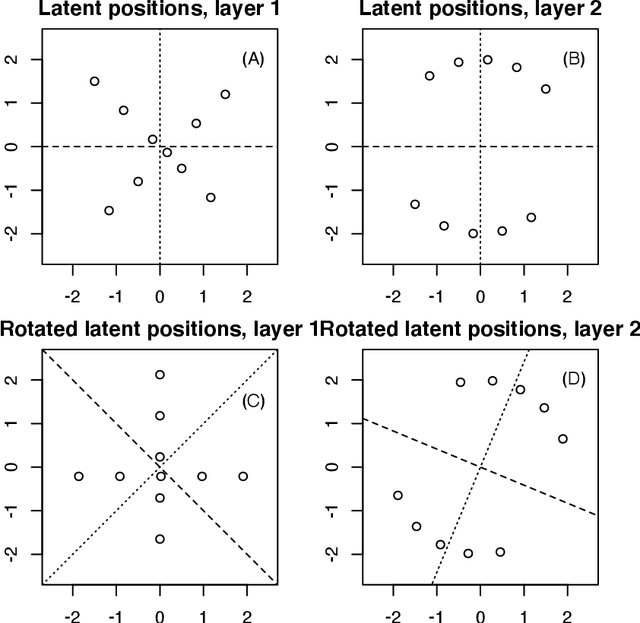
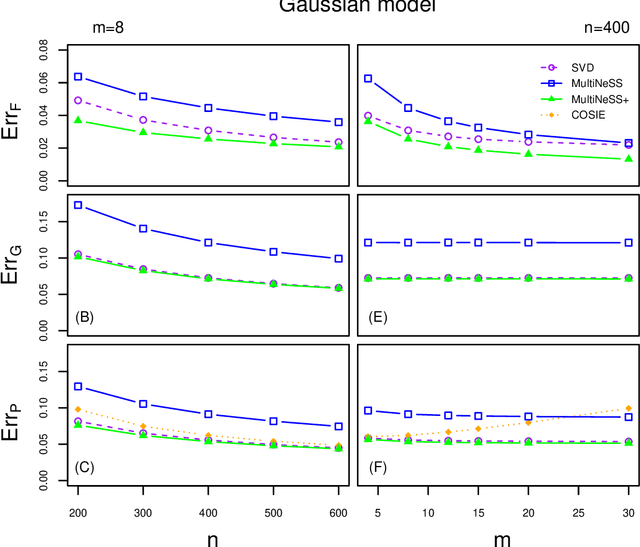
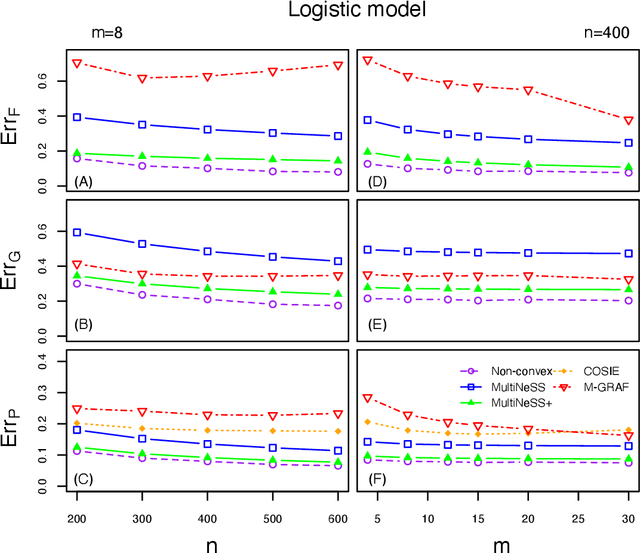
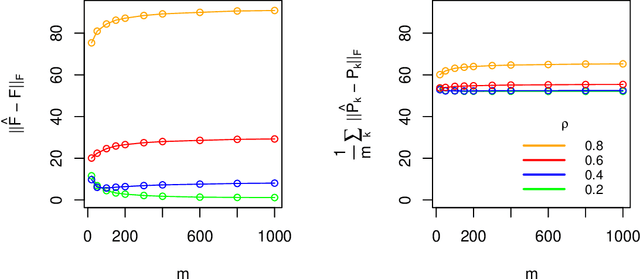
Latent space models are frequently used for modeling single-layer networks and include many popular special cases, such as the stochastic block model and the random dot product graph. However, they are not well-developed for more complex network structures, which are becoming increasingly common in practice. Here we propose a new latent space model for multiplex networks: multiple, heterogeneous networks observed on a shared node set. Multiplex networks can represent a network sample with shared node labels, a network evolving over time, or a network with multiple types of edges. The key feature of our model is that it learns from data how much of the network structure is shared between layers and pools information across layers as appropriate. We establish identifiability, develop a fitting procedure using convex optimization in combination with a nuclear norm penalty, and prove a guarantee of recovery for the latent positions as long as there is sufficient separation between the shared and the individual latent subspaces. We compare the model to competing methods in the literature on simulated networks and on a multiplex network describing the worldwide trade of agricultural products.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge