Is a good offensive always the best defense?
Paper and Code
Aug 23, 2016
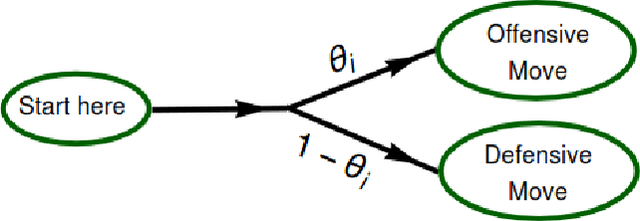

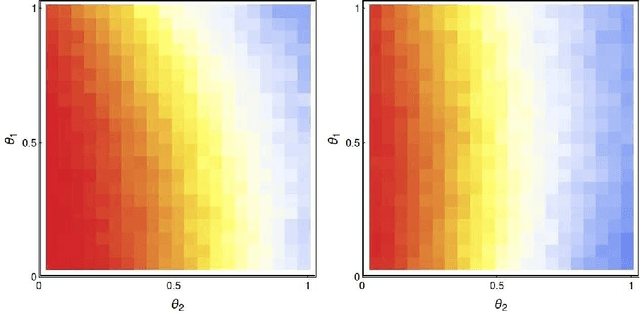
A checkers-like model game with a simplified set of rules is studied through extensive simulations of agents with different expertise and strategies. The introduction of complementary strategies, in a quite general way, provides a tool to mimic the basic ingredients of a wide scope of real games. We find that only for the player having the higher offensive expertise (the dominant player ), maximizing the offensive always increases the probability to win. For the non-dominant player, interestingly, a complete minimization of the offensive becomes the best way to win in many situations, depending on the relative values of the defense expertise. Further simulations on the interplay of defense expertise were done separately, in the context of a fully-offensive scenario, offering a starting point for analytical treatments. In particular, we established that in this scenario the total number of moves is defined only by the player with the lower defensive expertise. We believe that these results stand for a first step towards a new way to improve decisions-making in a large number of zero-sum real games.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge