Interpolation of CT Projections by Exploiting Their Self-Similarity and Smoothness
Paper and Code
Mar 05, 2021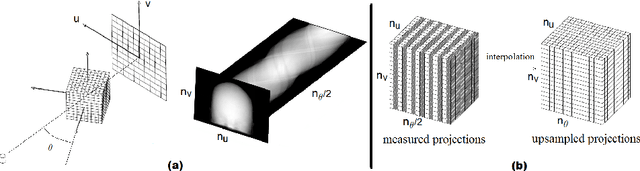
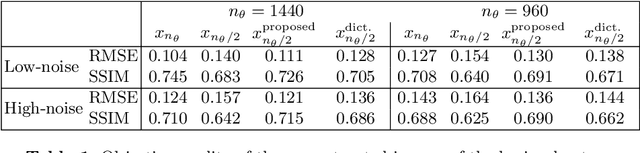
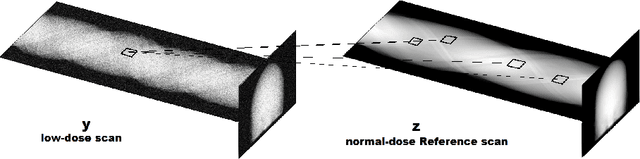
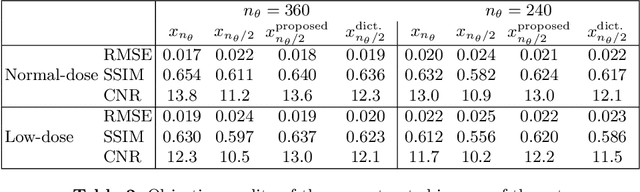
As the medical usage of computed tomography (CT) continues to grow, the radiation dose should remain at a low level to reduce the health risks. Therefore, there is an increasing need for algorithms that can reconstruct high-quality images from low-dose scans. In this regard, most of the recent studies have focused on iterative reconstruction algorithms, and little attention has been paid to restoration of the projection measurements, i.e., the sinogram. In this paper, we propose a novel sinogram interpolation algorithm. The proposed algorithm exploits the self-similarity and smoothness of the sinogram. Sinogram self-similarity is modeled in terms of the similarity of small blocks extracted from stacked projections. The smoothness is modeled via second-order total variation. Experiments with simulated and real CT data show that sinogram interpolation with the proposed algorithm leads to a substantial improvement in the quality of the reconstructed image, especially on low-dose scans. The proposed method can result in a significant reduction in the number of projection measurements. This will reduce the radiation dose and also the amount of data that need to be stored or transmitted, if the reconstruction is to be performed in a remote site.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge