Integrating connection search in graph queries
Paper and Code
Aug 09, 2022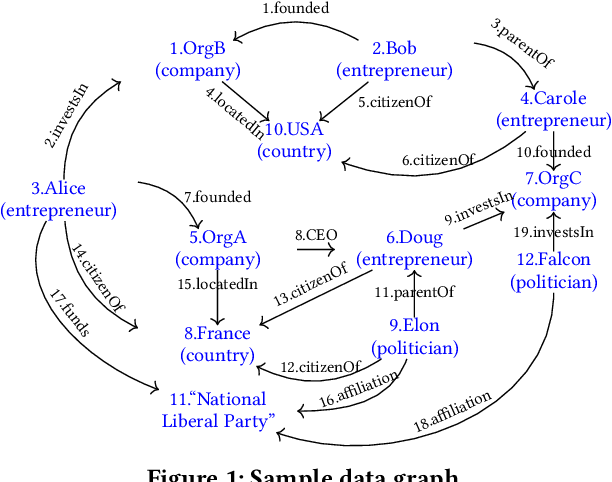

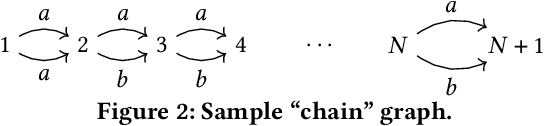
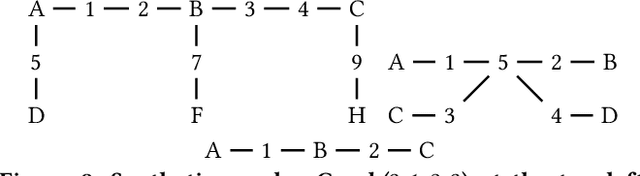
Graph data management and querying has many practical applications. When graphs are very heterogeneous and/or users are unfamiliar with their structure, they may need to find how two or more groups of nodes are connected in a graph, even when users are not able to describe the connections. This is only partially supported by existing query languages, which allow searching for paths, but not for trees connecting three or more node groups. The latter is related to the NP-hard Group Steiner Tree problem, and has been previously considered for keyword search in databases. In this work, we formally show how to integrate connecting tree patterns (CTPs, in short) within a graph query language such as SPARQL or Cypher, leading to an Extended Query Language (or EQL, in short). We then study a set of algorithms for evaluating CTPs; we generalize prior keyword search work, most importantly by (i) considering bidirectional edge traversal and (ii) allowing users to select any score function for ranking CTP results. To cope with very large search spaces, we propose an efficient pruning technique and formally establish a large set of cases where our algorithm, MOLESP, is complete even with pruning. Our experiments validate the performance of our CTP and EQL evaluation algorithms on a large set of synthetic and real-world workloads.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge