Idealized Dynamic Population Sizing for Uniformly Scaled Problems
Paper and Code
Apr 13, 2011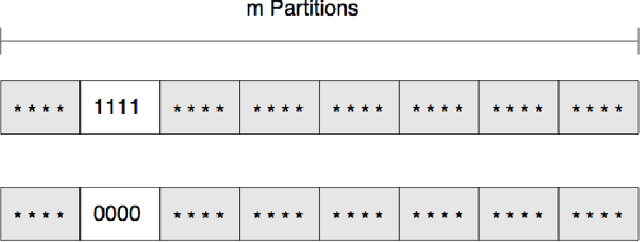
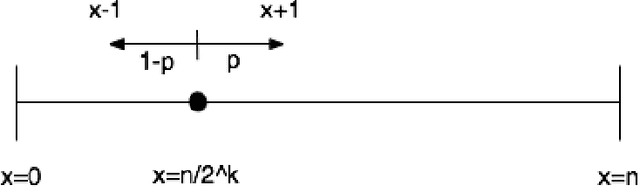
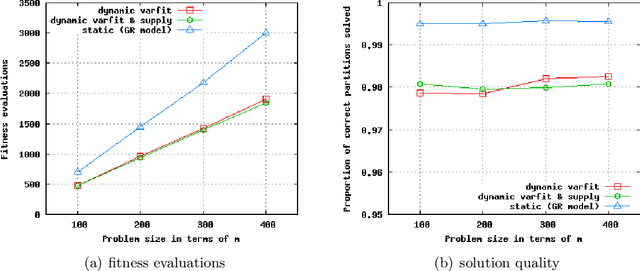
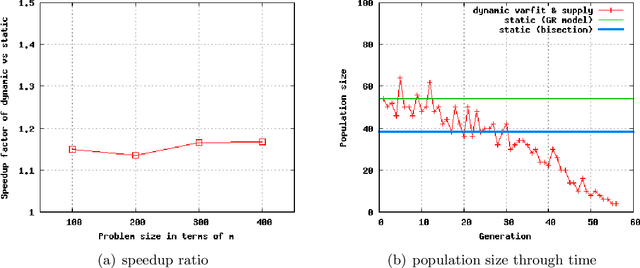
This paper explores an idealized dynamic population sizing strategy for solving additive decomposable problems of uniform scale. The method is designed on top of the foundations of existing population sizing theory for this class of problems, and is carefully compared with an optimal fixed population sized genetic algorithm. The resulting strategy should be close to a lower bound in terms of what can be achieved, performance-wise, by self-adjusting population sizing algorithms for this class of problems.
* 14 pages, submitted to ACM GECCO-2011
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge