Hypothesis Testing for Equality of Latent Positions in Random Graphs
Paper and Code
May 23, 2021
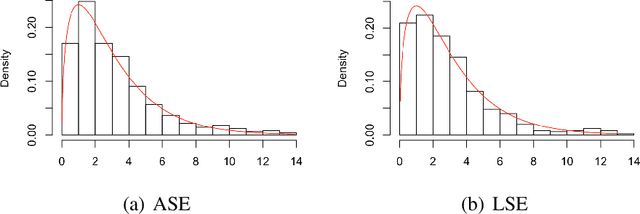
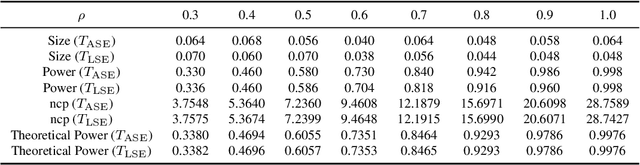
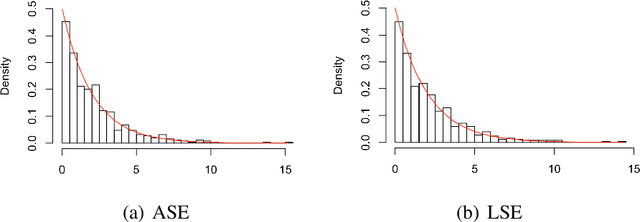
We consider the hypothesis testing problem that two vertices $i$ and $j$ of a generalized random dot product graph have the same latent positions, possibly up to scaling. Special cases of this hypotheses test include testing whether two vertices in a stochastic block model or degree-corrected stochastic block model graph have the same block membership vectors. We propose several test statistics based on the empirical Mahalanobis distances between the $i$th and $j$th rows of either the adjacency or the normalized Laplacian spectral embedding of the graph. We show that, under mild conditions, these test statistics have limiting chi-square distributions under both the null and local alternative hypothesis, and we derived explicit expressions for the non-centrality parameters under the local alternative. Using these limit results, we address the model selection problem of choosing between the standard stochastic block model and its degree-corrected variant. The effectiveness of our proposed tests are illustrated via both simulation studies and real data applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge