Hyperuniform scalar random fields for lensless, multispectral imaging systems
Paper and Code
Jul 15, 2021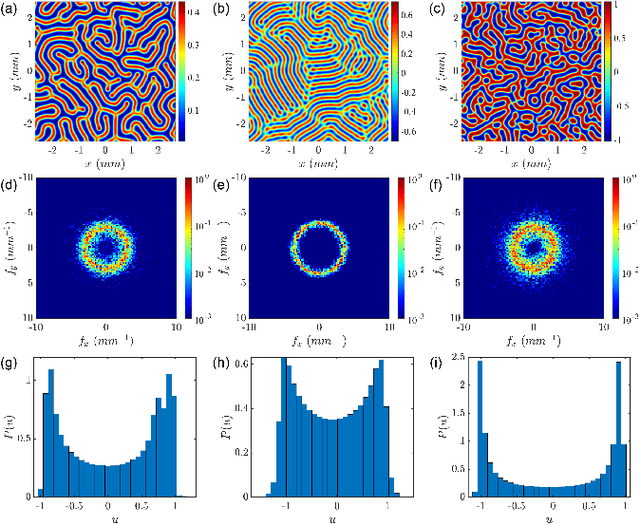
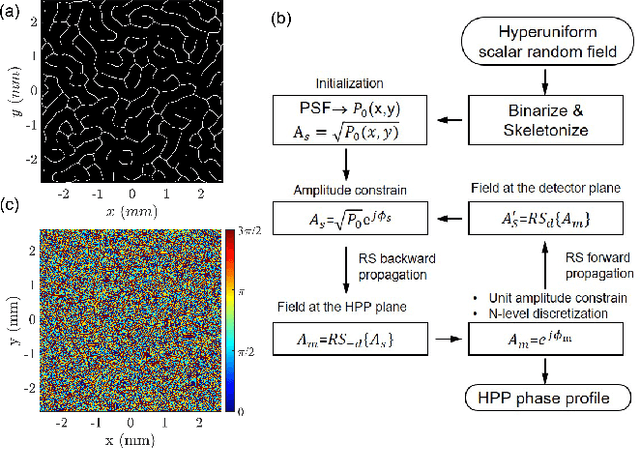
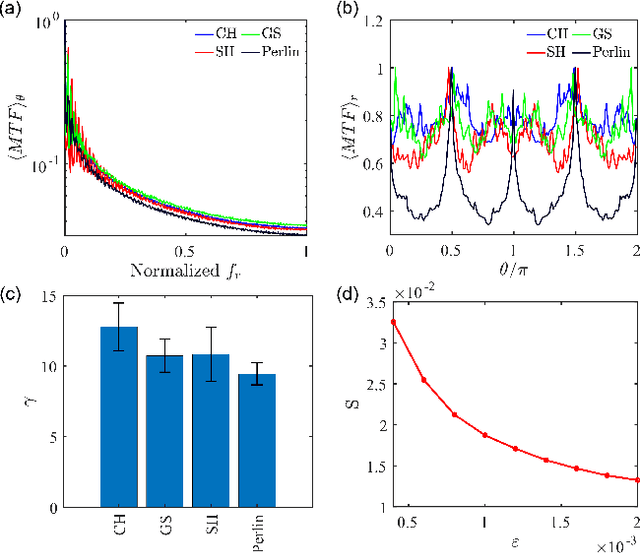
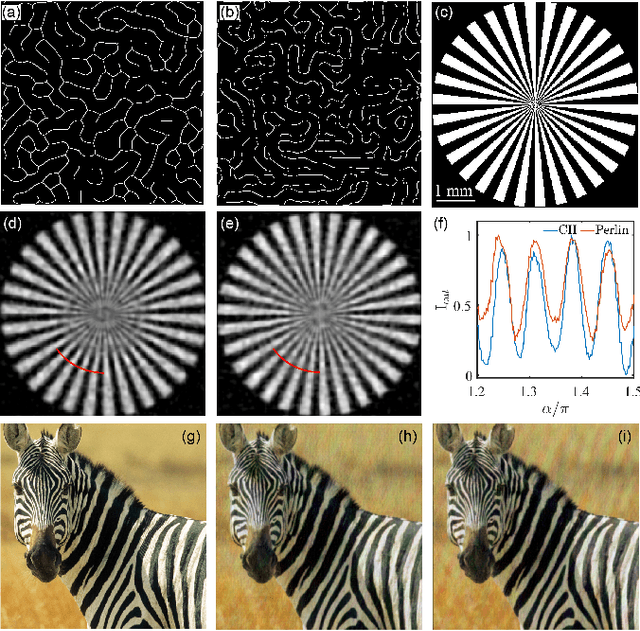
We propose a novel framework for the systematic design of lensless imaging systems based on the hyperuniform random field solutions of nonlinear reaction-diffusion equations from pattern formation theory. Specifically, we introduce a new class of imaging point-spread-functions (PSFs) with enhanced isotropic behavior and controllable sparsity. We investigate the PSFs and the modulated transfer functions (MTFs) for a number of nonlinear models and demonstrate that two-phase isotropic random fields with hyperuniform disorder are ideally suited to construct imaging PSFs with improved performances compared to PSFs based on the Perlin noise. Additionally, we introduce a phase retrieval algorithm based on the non-paraxial Rayleigh-Sommerfeld diffraction theory and introduce diffractive phase plates with PSFs designed from hyperuniform random fields, called hyperuniform phase plates (HPPs). Finally, using high-fidelity object reconstruction, we demonstrate improved image quality using engineered HPPs across the visible range. The proposed framework is suitable for high-performance lensless imaging systems for on-chip microscopy and spectroscopy applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge