How much do contextualized representations encode long-range context?
Paper and Code
Oct 16, 2024
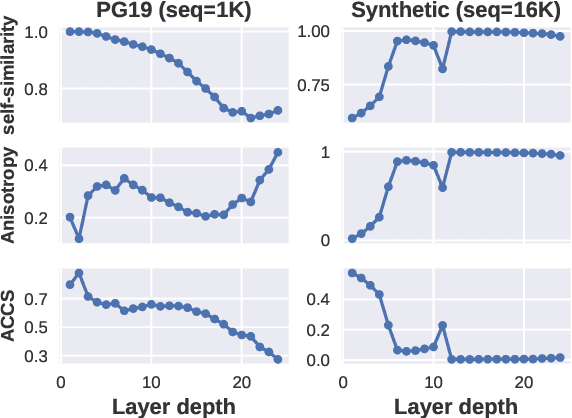
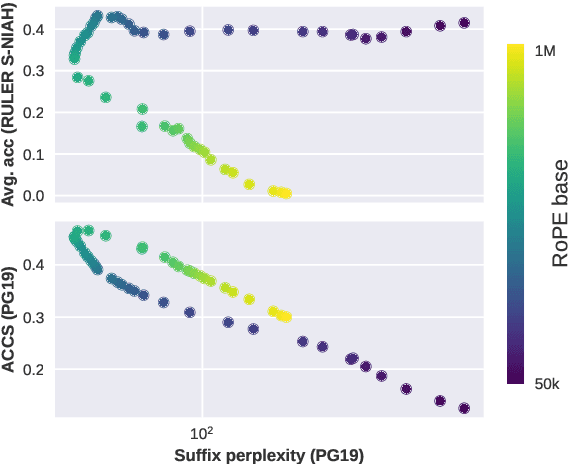
We analyze contextual representations in neural autoregressive language models, emphasizing long-range contexts that span several thousand tokens. Our methodology employs a perturbation setup and the metric \emph{Anisotropy-Calibrated Cosine Similarity}, to capture the degree of contextualization of long-range patterns from the perspective of representation geometry. We begin the analysis with a case study on standard decoder-only Transformers, demonstrating that similar perplexity can exhibit markedly different downstream task performance, which can be explained by the difference in contextualization of long-range content. Next, we extend the analysis to other models, covering recent novel architectural designs and various training configurations. The representation-level results illustrate a reduced capacity for high-complexity (i.e., less compressible) sequences across architectures, and that fully recurrent models rely heavily on local context, whereas hybrid models more effectively encode the entire sequence structure. Finally, preliminary analysis of model size and training configurations on the encoding of long-range context suggest potential directions for improving existing language models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge