Homology Computation of Large Point Clouds using Quantum Annealing
Paper and Code
Jun 06, 2016
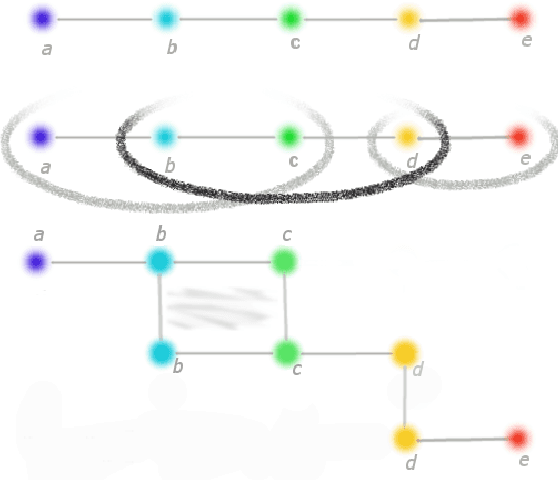
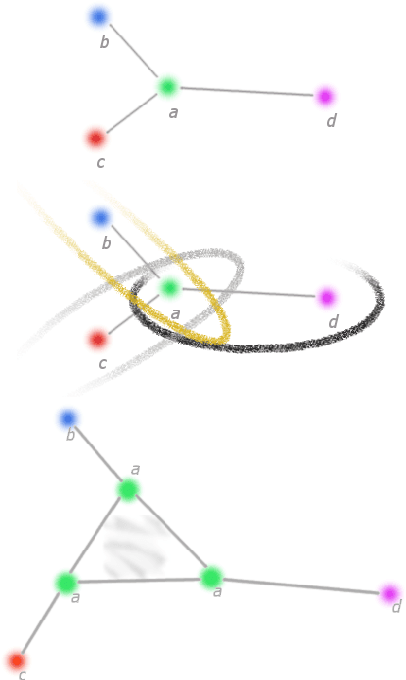
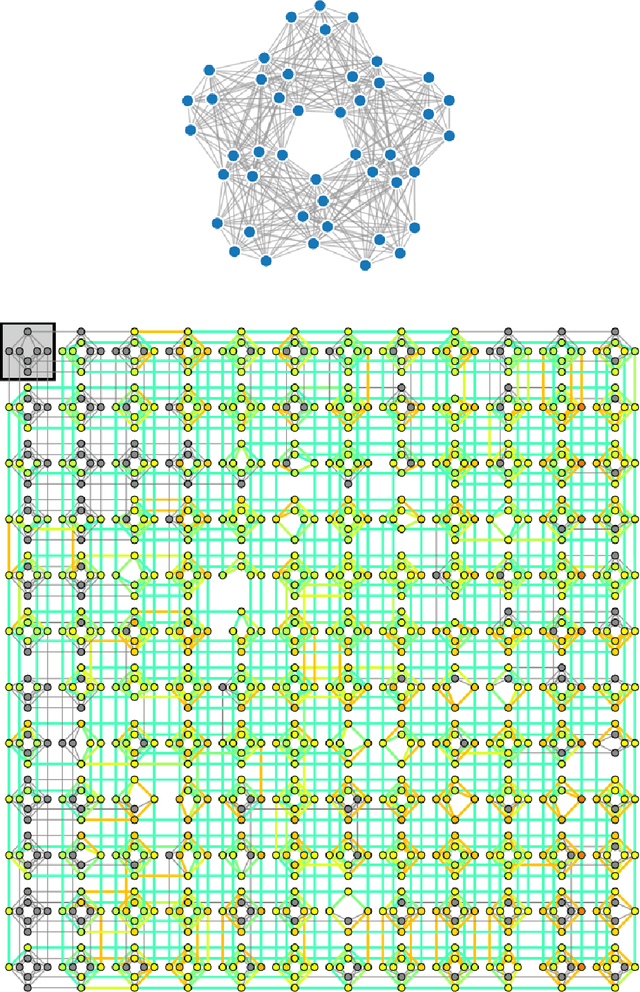
Homology is a tool in topological data analysis which measures the shape of the data. In many cases, these measurements translate into new insights which are not available by other means. To compute homology, we rely on mathematical constructions which scale exponentially with the size of the data. Therefore, for large point clouds, the computation is infeasible using classical computers. In this paper, we present a quantum annealing pipeline for computation of homology of large point clouds. The pipeline takes as input a graph approximating the given point cloud. It uses quantum annealing to compute a clique covering of the graph and then uses this cover to construct a Mayer-Vietoris complex. The pipeline terminates by performing a simplified homology computation of the Mayer-Vietoris complex. We have introduced three different clique coverings and their quantum annealing formulation. Our pipeline scales polynomially in the size of the data, once the covering step is solved. To prove correctness of our algorithm, we have also included tests using D-Wave 2X quantum processor.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge