Homography Decomposition Networks for Planar Object Tracking
Paper and Code
Dec 27, 2021
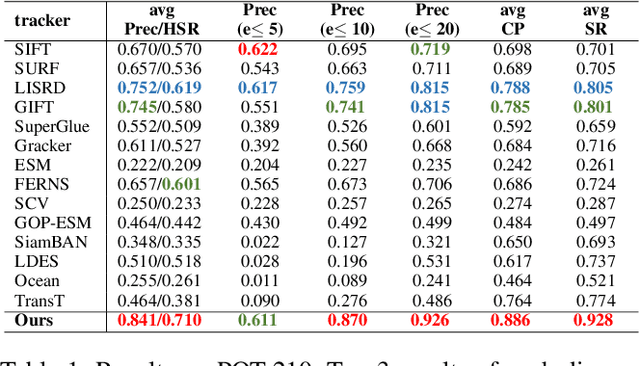
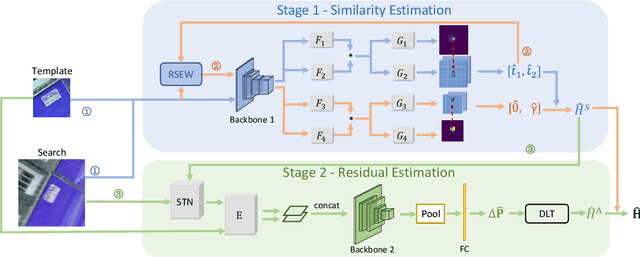
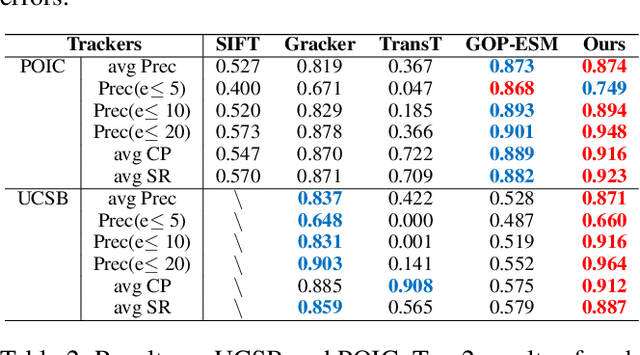
Planar object tracking plays an important role in AI applications, such as robotics, visual servoing, and visual SLAM. Although the previous planar trackers work well in most scenarios, it is still a challenging task due to the rapid motion and large transformation between two consecutive frames. The essential reason behind this problem is that the condition number of such a non-linear system changes unstably when the searching range of the homography parameter space becomes larger. To this end, we propose a novel Homography Decomposition Networks(HDN) approach that drastically reduces and stabilizes the condition number by decomposing the homography transformation into two groups. Specifically, a similarity transformation estimator is designed to predict the first group robustly by a deep convolution equivariant network. By taking advantage of the scale and rotation estimation with high confidence, a residual transformation is estimated by a simple regression model. Furthermore, the proposed end-to-end network is trained in a semi-supervised fashion. Extensive experiments show that our proposed approach outperforms the state-of-the-art planar tracking methods at a large margin on the challenging POT, UCSB and POIC datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge