Hindsight Network Credit Assignment: Efficient Credit Assignment in Networks of Discrete Stochastic Units

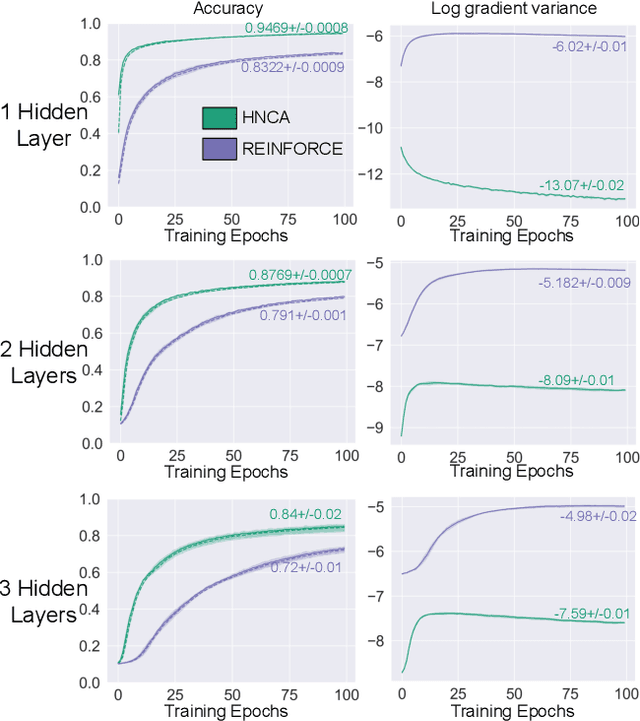
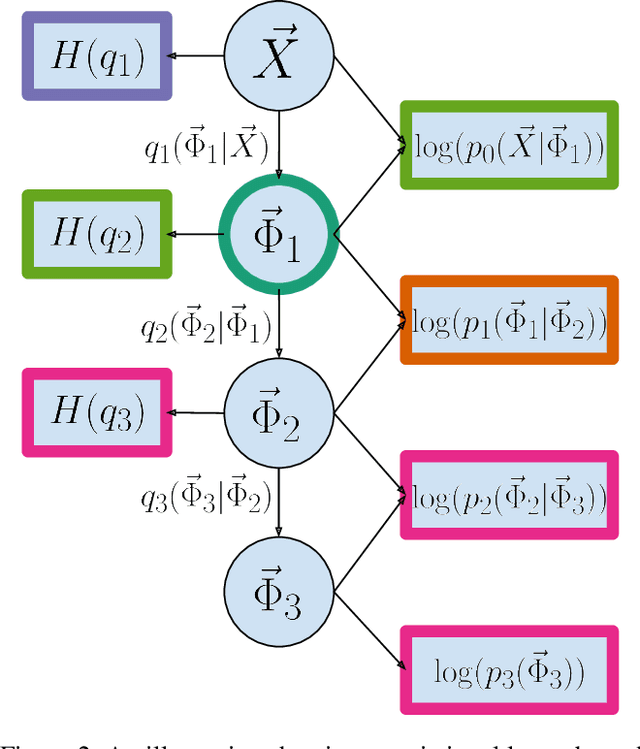
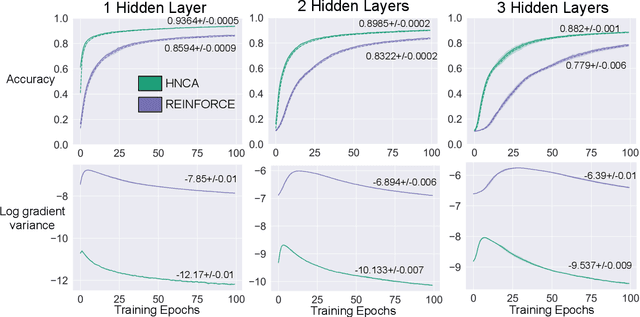
Training neural networks with discrete stochastic variables presents a unique challenge. Backpropagation is not directly applicable, nor are the reparameterization tricks used in networks with continuous stochastic variables. To address this challenge, we present Hindsight Network Credit Assignment (HNCA), a novel learning algorithm for networks of discrete stochastic units. HNCA works by assigning credit to each unit based on the degree to which its output influences its immediate children in the network. We prove that HNCA produces unbiased gradient estimates with reduced variance compared to the REINFORCE estimator, while the computational cost is similar to that of backpropagation. We first apply HNCA in a contextual bandit setting to optimize a reward function that is unknown to the agent. In this setting, we empirically demonstrate that HNCA significantly outperforms REINFORCE, indicating that the variance reduction implied by our theoretical analysis is significant and impactful. We then show how HNCA can be extended to optimize a more general function of the outputs of a network of stochastic units, where the function is known to the agent. We apply this extended version of HNCA to train a discrete variational auto-encoder and empirically show it compares favourably to other strong methods. We believe that the ideas underlying HNCA can help stimulate new ways of thinking about efficient credit assignment in stochastic compute graphs.