Higher-order interactions in statistical physics and machine learning: A non-parametric solution to the inverse problem

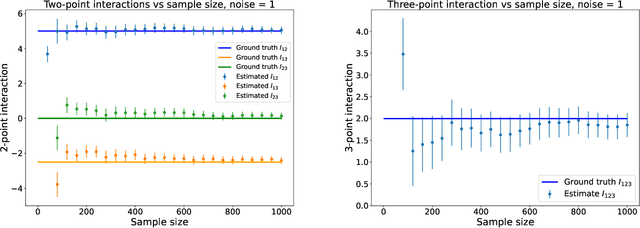
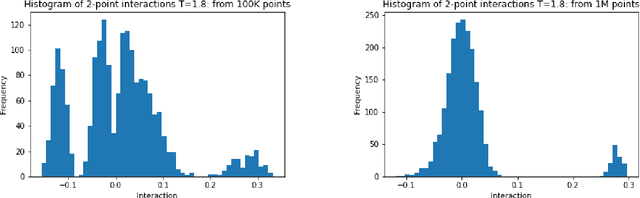
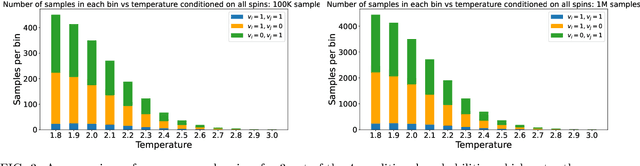
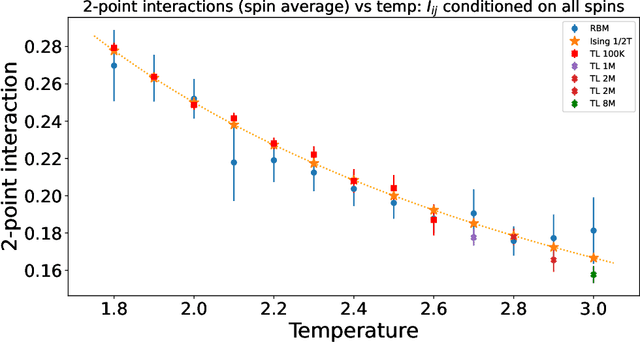
We propose a model-independent definition of $n$-point interaction within a system of binary and categorical random variables from first principles, via the non-parametric framework of Targeted Learning, a subfield of mathematical statistics. This definition provides an interpretation for both magnitude and sign of $2$-point, $3$-point, and general $n$-point interactions. We show that the sign of an $n$-point interaction is interpretable relative to an $(n-1)$-point interaction obtained by fixing any one of the $n$ variables. The non-parametric definition of interaction is fundamentally unbiased and reduces to familiar notions of interaction in parametric statistical physics models. Moreover, by taking into account information on conditional independence and without any further assumptions, the accuracy of interactions estimated directly from data is substantially increased whilst the number of samples required and the computational run time are both reduced. We illustrate these concepts both analytically and numerically on (i) the $2$-dimensional Ising model, (ii) an Ising-like model with non-zero $2$-point, $3$-point, and $4$-point interactions, (iii) the Restricted Boltzmann Machine (RBM), and argue that the formulation applies to energy-based models more generally. The non-parametric formulation allows for the direct reconstruction of the Hamiltonian from the data it generated. Finally, we discuss novel applications of this work, namely estimating causal molecular interactions leading to physiological outcomes, in population biomedicine.