HCNAF: Hyper-Conditioned Neural Autoregressive Flow and its Application for Probabilistic Occupancy Map Forecasting

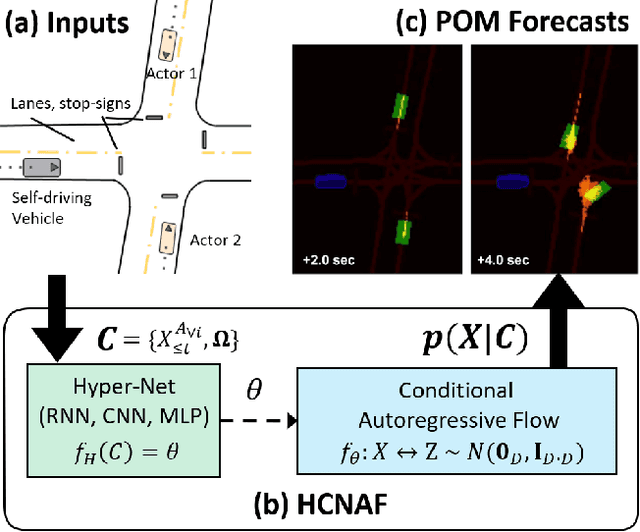
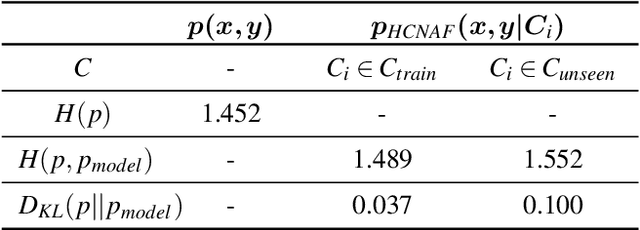
We introduce Hyper-Conditioned Neural Autoregressive Flow (HCNAF); a powerful universal distribution approximator designed to model arbitrarily complex conditional probability density functions. HCNAF consists of a neural-net based conditional autoregressive flow (AF) and a hyper-network that can take large conditions in non-autoregressive fashion and outputs the network parameters of the AF. Like other flow models, HCNAF performs exact likelihood inference. We demonstrate the effectiveness and attributes of HCNAF, including its generalization capability over unseen conditions and show that HCNAF outperforms recent flow models in a conditional density estimation task for MNIST. We also show that HCNAF scales up to complex high-dimensional prediction problems of the magnitude of self-driving and that HCNAF yields a state-of-the-art performance in a public self-driving dataset.