Graph Neural Networks with Parallel Neighborhood Aggregations for Graph Classification
Paper and Code
Nov 22, 2021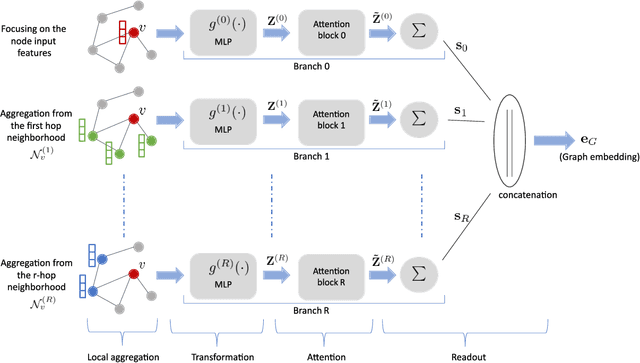

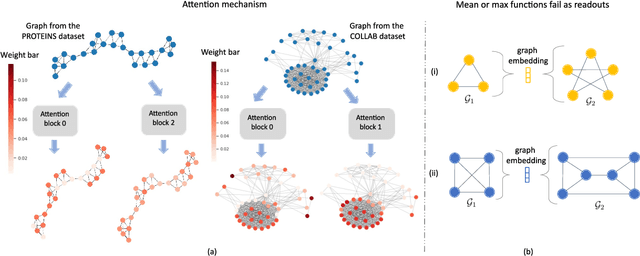
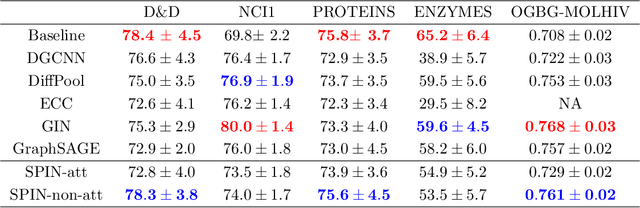
We focus on graph classification using a graph neural network (GNN) model that precomputes the node features using a bank of neighborhood aggregation graph operators arranged in parallel. These GNN models have a natural advantage of reduced training and inference time due to the precomputations but are also fundamentally different from popular GNN variants that update node features through a sequential neighborhood aggregation procedure during training. We provide theoretical conditions under which a generic GNN model with parallel neighborhood aggregations (PA-GNNs, in short) are provably as powerful as the well-known Weisfeiler-Lehman (WL) graph isomorphism test in discriminating non-isomorphic graphs. Although PA-GNN models do not have an apparent relationship with the WL test, we show that the graph embeddings obtained from these two methods are injectively related. We then propose a specialized PA-GNN model, called SPIN, which obeys the developed conditions. We demonstrate via numerical experiments that the developed model achieves state-of-the-art performance on many diverse real-world datasets while maintaining the discriminative power of the WL test and the computational advantage of preprocessing graphs before the training process.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge