Graph Learning for Inverse Landscape Genetics

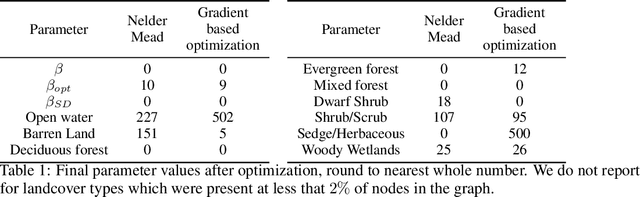
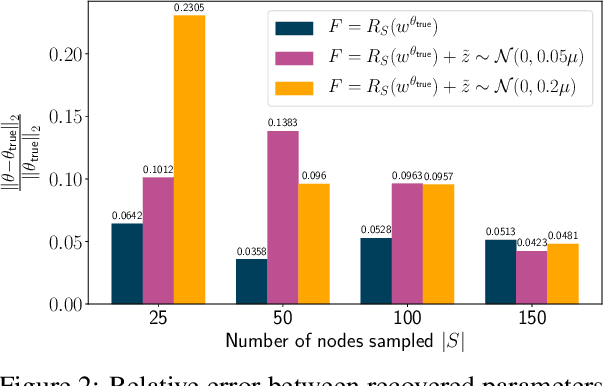
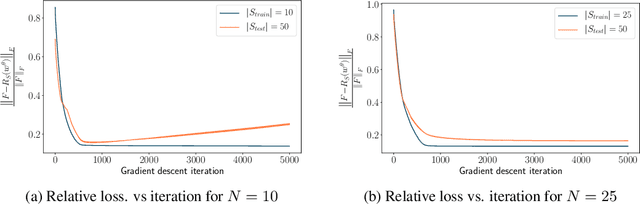
The problem of inferring unknown graph edges from numerical data at a graph's nodes appears in many forms across machine learning. We study a version of this problem that arises in the field of landscape genetics, where genetic similarity between populations of organisms living in a heterogeneous landscape is explained by a weighted graph that encodes the ease of dispersal through that landscape. Our main contribution is an efficient algorithm for inverse landscape genetics, which is the task of inferring this graph from measurements of genetic similarity at different locations (graph nodes). We reduced the problem to that of inferring graph edges from noisy measurements of effective resistances between graph nodes, which have been observed to correlate well with genetic similarity. Building on Hoskins et. al., we develop an efficient first-order optimization method for solving this problem. Despite its non-convex nature, extensive experiments on synthetic and real genetic data establish that our method provides fast and reliable convergence, significantly outperforming existing heuristics used in the field.