Going Beyond Approximation: Encoding Constraints for Explainable Multi-hop Inference via Differentiable Combinatorial Solvers
Paper and Code
Aug 05, 2022
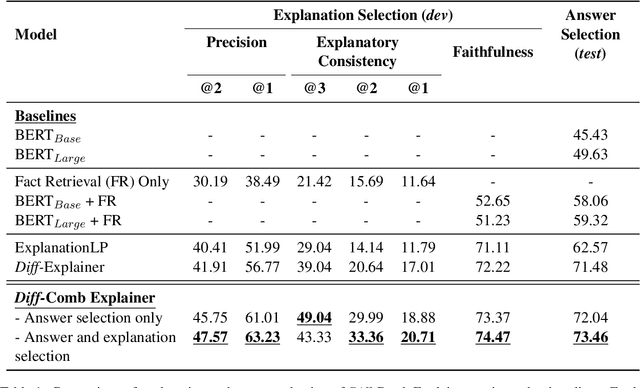


Integer Linear Programming (ILP) provides a viable mechanism to encode explicit and controllable assumptions about explainable multi-hop inference with natural language. However, an ILP formulation is non-differentiable and cannot be integrated into broader deep learning architectures. Recently, Thayaparan et al. (2021a) proposed a novel methodology to integrate ILP with Transformers to achieve end-to-end differentiability for complex multi-hop inference. While this hybrid framework has been demonstrated to deliver better answer and explanation selection than transformer-based and existing ILP solvers, the neuro-symbolic integration still relies on a convex relaxation of the ILP formulation, which can produce sub-optimal solutions. To improve these limitations, we propose Diff-Comb Explainer, a novel neuro-symbolic architecture based on Differentiable BlackBox Combinatorial solvers (DBCS) (Pogan\v{c}i\'c et al., 2019). Unlike existing differentiable solvers, the presented model does not require the transformation and relaxation of the explicit semantic constraints, allowing for direct and more efficient integration of ILP formulations. Diff-Comb Explainer demonstrates improved accuracy and explainability over non-differentiable solvers, Transformers and existing differentiable constraint-based multi-hop inference frameworks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge