Globally Optimal Gradient Descent for a ConvNet with Gaussian Inputs
Paper and Code
Feb 26, 2017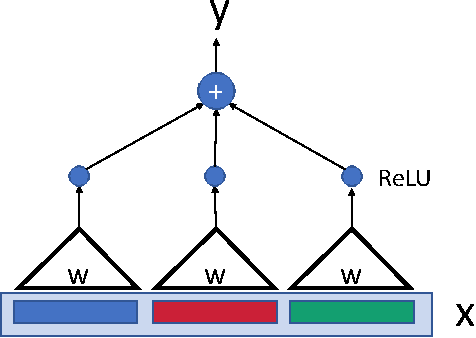

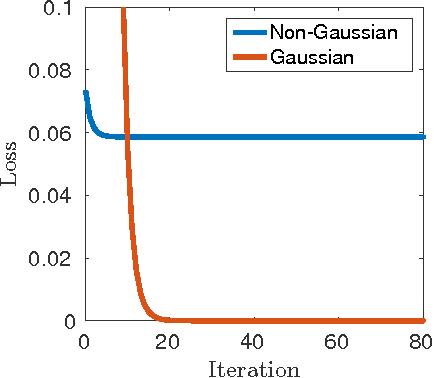
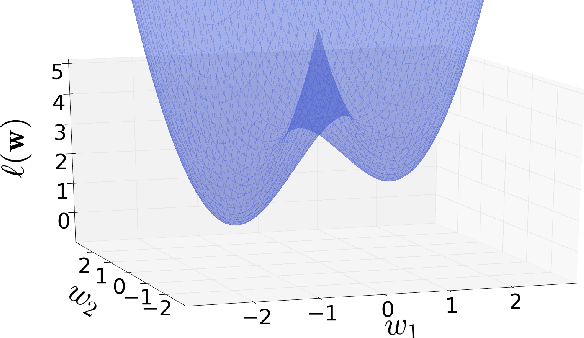
Deep learning models are often successfully trained using gradient descent, despite the worst case hardness of the underlying non-convex optimization problem. The key question is then under what conditions can one prove that optimization will succeed. Here we provide a strong result of this kind. We consider a neural net with one hidden layer and a convolutional structure with no overlap and a ReLU activation function. For this architecture we show that learning is NP-complete in the general case, but that when the input distribution is Gaussian, gradient descent converges to the global optimum in polynomial time. To the best of our knowledge, this is the first global optimality guarantee of gradient descent on a convolutional neural network with ReLU activations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge