Geometry of energy landscapes and the optimizability of deep neural networks

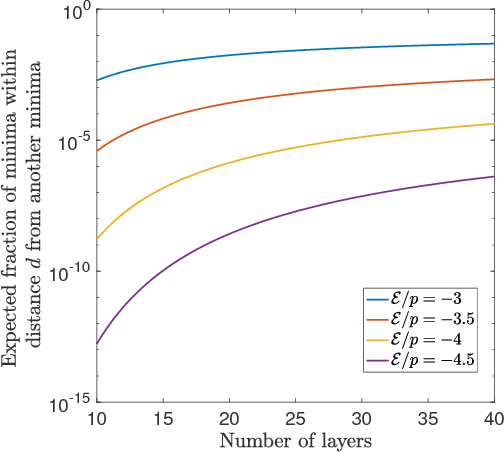
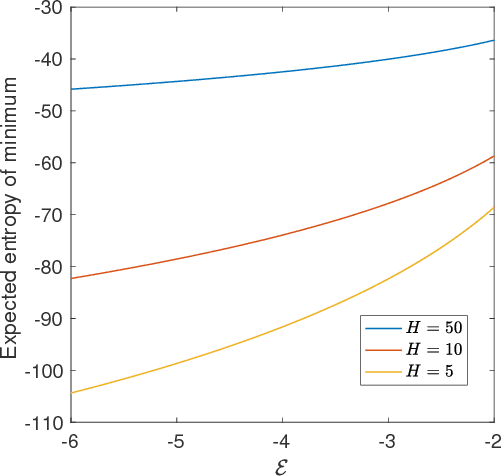
Deep neural networks are workhorse models in machine learning with multiple layers of non-linear functions composed in series. Their loss function is highly non-convex, yet empirically even gradient descent minimisation is sufficient to arrive at accurate and predictive models. It is hitherto unknown why are deep neural networks easily optimizable. We analyze the energy landscape of a spin glass model of deep neural networks using random matrix theory and algebraic geometry. We analytically show that the multilayered structure holds the key to optimizability: Fixing the number of parameters and increasing network depth, the number of stationary points in the loss function decreases, minima become more clustered in parameter space, and the tradeoff between the depth and width of minima becomes less severe. Our analytical results are numerically verified through comparison with neural networks trained on a set of classical benchmark datasets. Our model uncovers generic design principles of machine learning models.