General stochastic separation theorems with optimal bounds
Paper and Code
Oct 11, 2020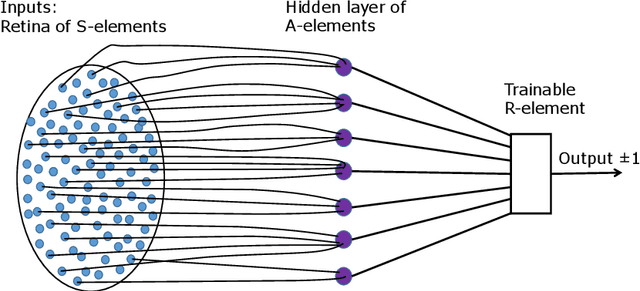
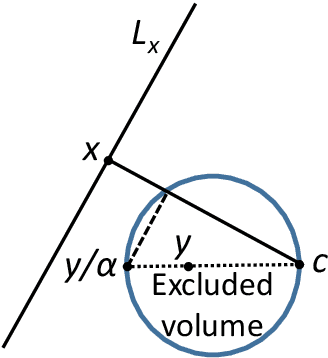
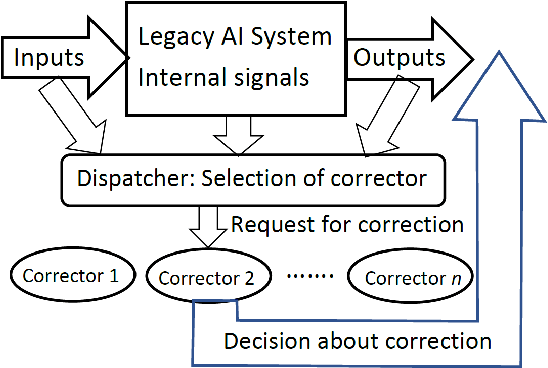
Phenomenon of stochastic separability was revealed and used in machine learning to correct errors of Artificial Intelligence (AI) systems and analyze AI instabilities. In high-dimensional datasets under broad assumptions each point can be separated from the rest of the set by simple and robust Fisher's discriminant (is Fisher separable). Errors or clusters of errors can be separated from the rest of the data. The ability to correct an AI system also opens up the possibility of an attack on it, and the high dimensionality induces vulnerabilities caused by the same stochastic separability that holds the keys to understanding the fundamentals of robustness and adaptivity in high-dimensional data-driven AI. To manage errors and analyze vulnerabilities, the stochastic separation theorems should evaluate the probability that the dataset will be Fisher separable in given dimensionality and for a given class of distributions. Explicit and optimal estimates of these separation probabilities are required, and this problem is solved in present work. The general stochastic separation theorems with optimal probability estimates are obtained for important classes of distributions: log-concave distribution, their convex combinations and product distributions. The standard i.i.d. assumption was significantly relaxed. These theorems and estimates can be used both for correction of high-dimensional data driven AI systems and for analysis of their vulnerabilities. The third area of application is the emergence of memories in ensembles of neurons, the phenomena of grandmother's cells and sparse coding in the brain, and explanation of unexpected effectiveness of small neural ensembles in high-dimensional brain.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge