Fuzzy-Based Dialectical Non-Supervised Image Classification and Clustering
Paper and Code
Dec 03, 2017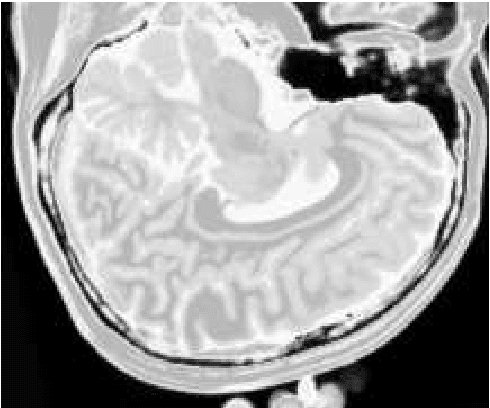
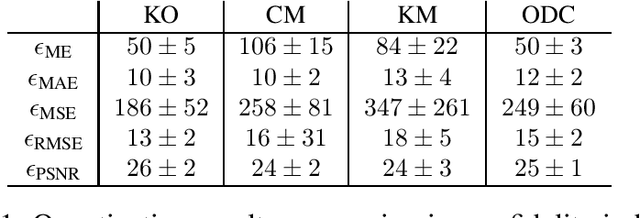
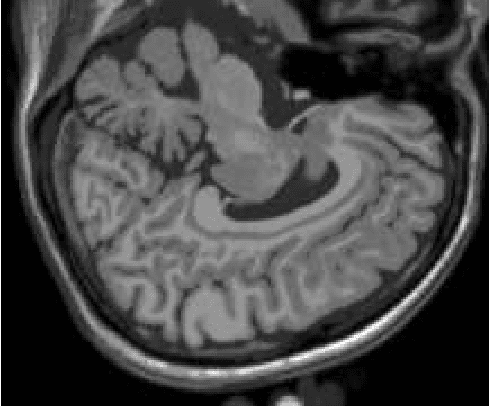
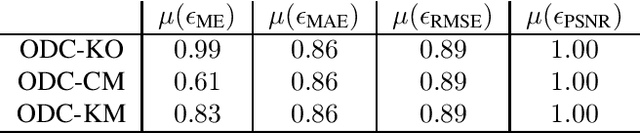
The materialist dialectical method is a philosophical investigative method to analyze aspects of reality. These aspects are viewed as complex processes composed by basic units named poles, which interact with each other. Dialectics has experienced considerable progress in the 19th century, with Hegel's dialectics and, in the 20th century, with the works of Marx, Engels, and Gramsci, in Philosophy and Economics. The movement of poles through their contradictions is viewed as a dynamic process with intertwined phases of evolution and revolutionary crisis. In order to build a computational process based on dialectics, the interaction between poles can be modeled using fuzzy membership functions. Based on this assumption, we introduce the Objective Dialectical Classifier (ODC), a non-supervised map for classification based on materialist dialectics and designed as an extension of fuzzy c-means classifier. As a case study, we used ODC to classify 181 magnetic resonance synthetic multispectral images composed by proton density, $T_1$- and $T_2$-weighted synthetic brain images. Comparing ODC to k-means, fuzzy c-means, and Kohonen's self-organized maps, concerning with image fidelity indexes as estimatives of quantization distortion, we proved that ODC can reach almost the same quantization performance as optimal non-supervised classifiers like Kohonen's self-organized maps.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge