From ChebNet to ChebGibbsNet
Paper and Code
Dec 02, 2024
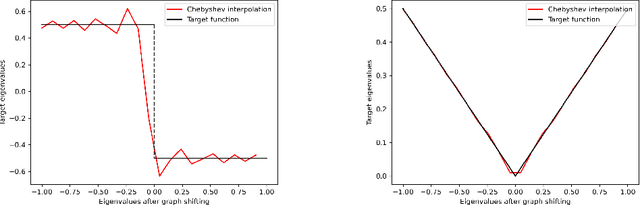

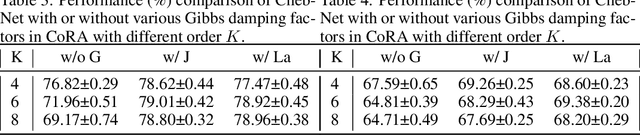
Recent advancements in Spectral Graph Convolutional Networks (SpecGCNs) have led to state-of-the-art performance in various graph representation learning tasks. To exploit the potential of SpecGCNs, we analyze corresponding graph filters via polynomial interpolation, the cornerstone of graph signal processing. Different polynomial bases, such as Bernstein, Chebyshev, and monomial basis, have various convergence rates that will affect the error in polynomial interpolation. Although adopting Chebyshev basis for interpolation can minimize maximum error, the performance of ChebNet is still weaker than GPR-GNN and BernNet. \textbf{We point out it is caused by the Gibbs phenomenon, which occurs when the graph frequency response function approximates the target function.} It reduces the approximation ability of a truncated polynomial interpolation. In order to mitigate the Gibbs phenomenon, we propose to add the Gibbs damping factor with each term of Chebyshev polynomials on ChebNet. As a result, our lightweight approach leads to a significant performance boost. Afterwards, we reorganize ChebNet via decoupling feature propagation and transformation. We name this variant as \textbf{ChebGibbsNet}. Our experiments indicate that ChebGibbsNet is superior to other advanced SpecGCNs, such as GPR-GNN and BernNet, in both homogeneous graphs and heterogeneous graphs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge