Founded Semantics and Constraint Semantics of Logic Rules

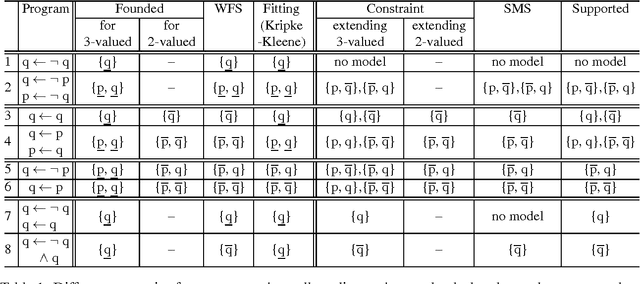
This paper describes a simple new semantics for logic rules, founded semantics, and its straightforward extension to another simple new semantics, constraint semantics. The new semantics support unrestricted negation, as well as unrestricted existential and universal quantifications. They are uniquely expressive and intuitive by allowing assumptions about the predicates and rules to be specified explicitly. They are completely declarative and easy to understand and relate cleanly to prior semantics. In addition, founded semantics can be computed in linear time in the size of the ground program.