Flow Segmentation in Dense Crowds

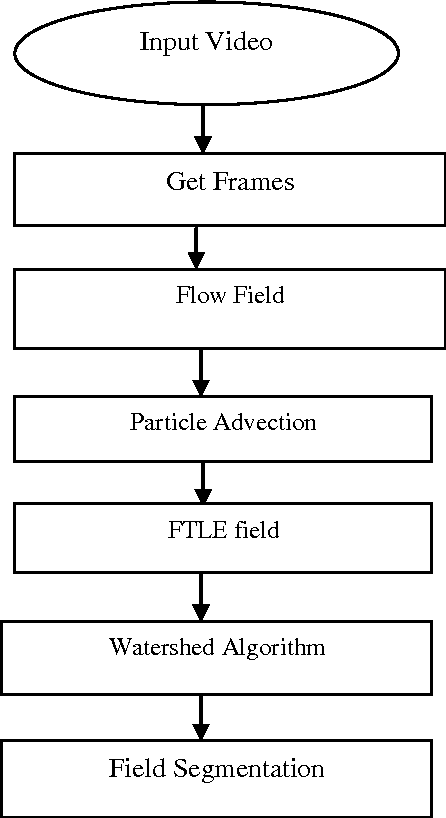
A framework is proposed in this paper that is used to segment flow of dense crowds. The flow field that is generated by the movement in the crowd is treated just like an aperiodic dynamic system. On this flow field a grid of particles is put over for particle advection by the use of a numerical integration scheme. Then flow maps are generated which associates the initial position of the particles with final position. The gradient of the flow maps gives the amount of divergence of the neighboring particles. For forward integration and analysis forward Finite time Lyapunov Exponent is calculated and backward Finite time Lyapunov Exponent is also calculated it gives the Lagrangian coherent structures of the flow in crowd. Lagrangian Coherent Structures basically divides the flow in crowd into regions and these regions have different dynamics. These regions are then used to get the boundary in the different flow segments by using water shed algorithm. The experiment is conducted on the crowd dataset of UCF (University of central Florida).