Exploiting Functional Dependencies in Qualitative Probabilistic Reasoning
Paper and Code
Mar 27, 2013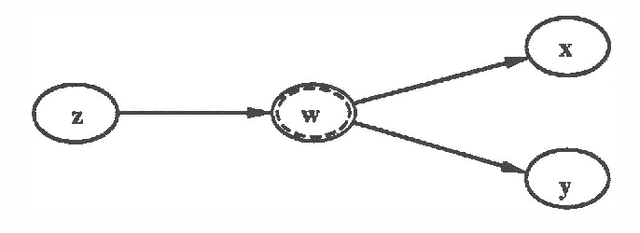
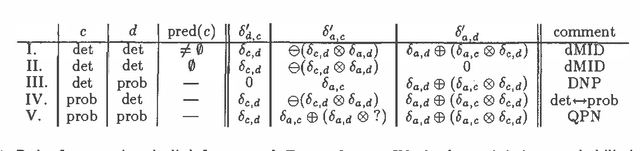


Functional dependencies restrict the potential interactions among variables connected in a probabilistic network. This restriction can be exploited in qualitative probabilistic reasoning by introducing deterministic variables and modifying the inference rules to produce stronger conclusions in the presence of functional relations. I describe how to accomplish these modifications in qualitative probabilistic networks by exhibiting the update procedures for graphical transformations involving probabilistic and deterministic variables and combinations. A simple example demonstrates that the augmented scheme can reduce qualitative ambiguity that would arise without the special treatment of functional dependency. Analysis of qualitative synergy reveals that new higher-order relations are required to reason effectively about synergistic interactions among deterministic variables.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge