Expectation propagation: a probabilistic view of Deep Feed Forward Networks

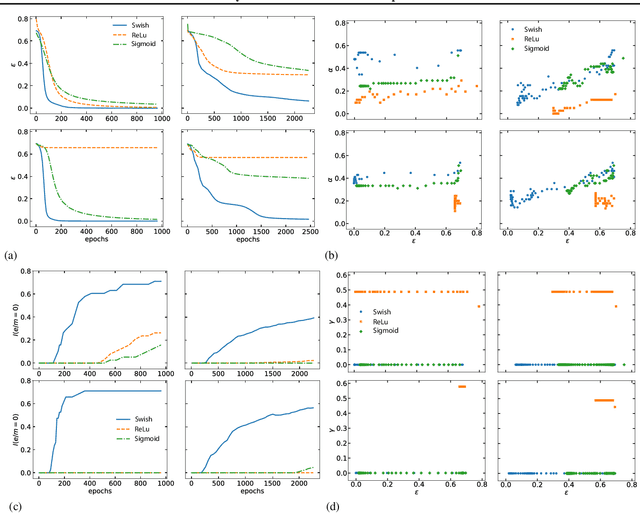
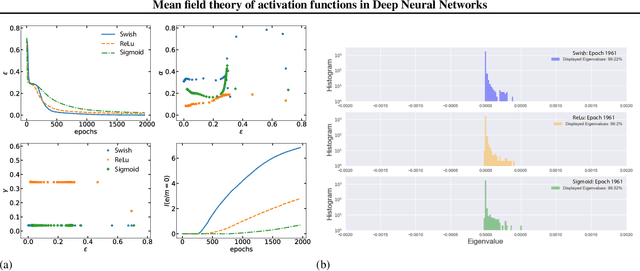
We present a statistical mechanics model of deep feed forward neural networks (FFN). Our energy-based approach naturally explains several known results and heuristics, providing a solid theoretical framework and new instruments for a systematic development of FFN. We infer that FFN can be understood as performing three basic steps: encoding, representation validation and propagation. We obtain a set of natural activations -- such as sigmoid, $\tanh$ and ReLu -- together with a state-of-the-art one, recently obtained by Ramachandran et al.(arXiv:1710.05941) using an extensive search algorithm. We term this activation ESP (Expected Signal Propagation), explain its probabilistic meaning, and study the eigenvalue spectrum of the associated Hessian on classification tasks. We find that ESP allows for faster training and more consistent performances over a wide range of network architectures.