Exchangeability, Conformal Prediction, and Rank Tests
Paper and Code
May 13, 2020
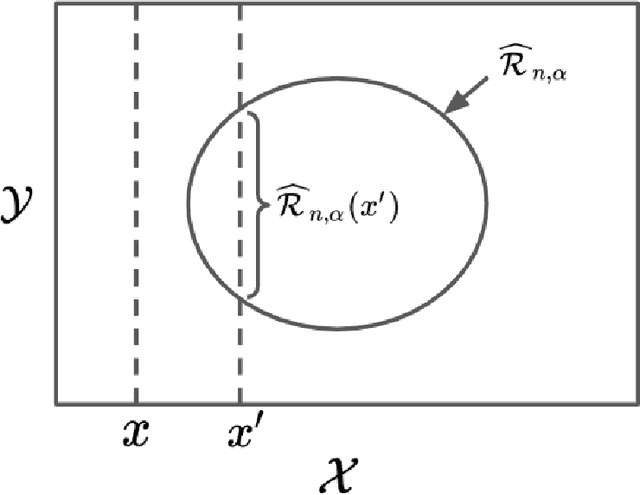
Conformal prediction has been a very popular method of distribution-free predictive inference in recent years in machine learning and statistics. The main reason for its popularity comes from the fact that it works as a wrapper around any prediction algorithm such as neural networks or random forests. Exchangeability is at the core of the validity of conformal prediction. The concept of exchangeability is also at the core of rank tests widely known in nonparametric statistics. In this paper, we review the concept of exchangeability and discuss its implications for rank tests and conformal prediction. Although written as an exposition, the main message of the paper is to show that similar to conformal prediction, rank tests can also be used as a wrapper around any dimension reduction algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge