Evaluating Generative Adversarial Networks on Explicitly Parameterized Distributions
Paper and Code
Dec 27, 2018
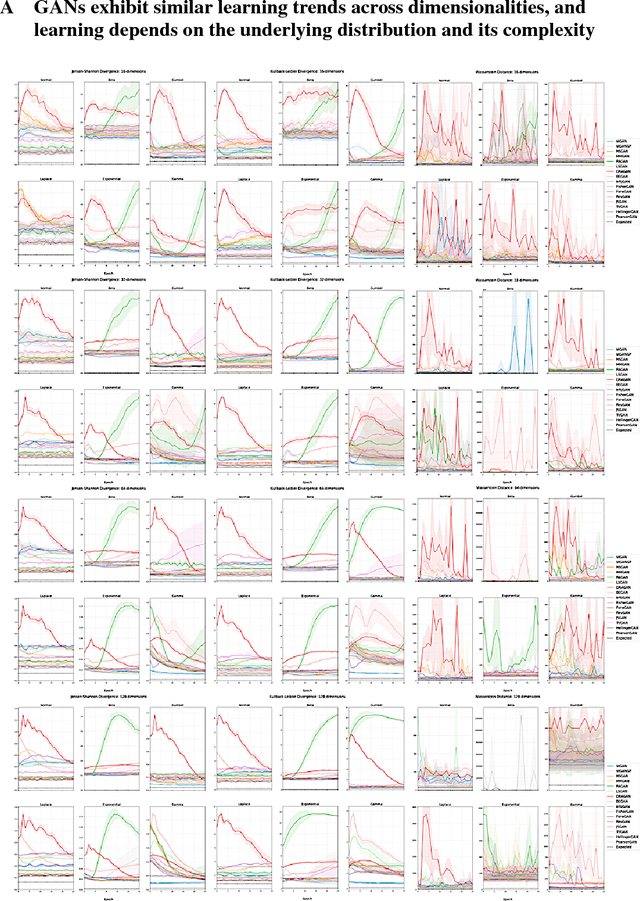
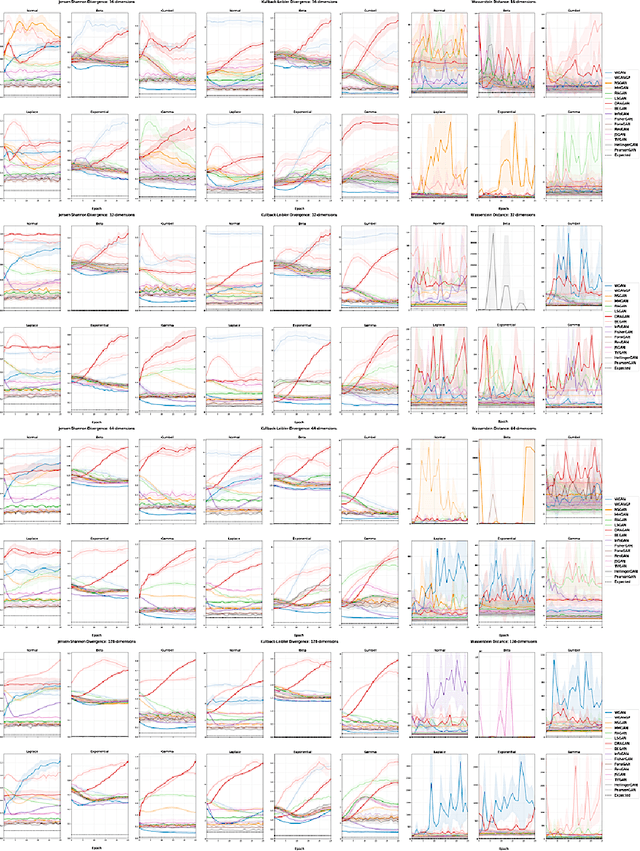
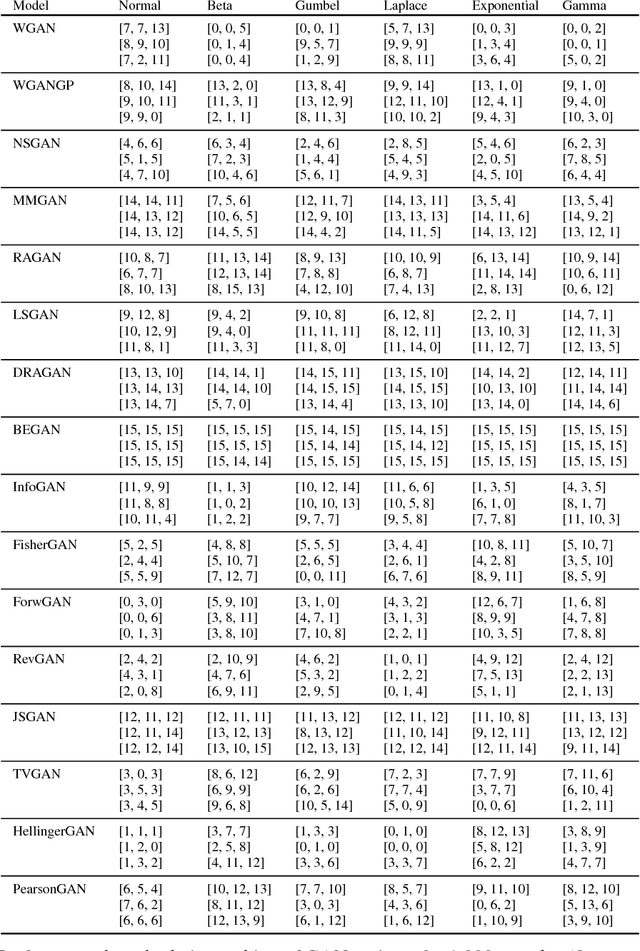
The true distribution parameterizations of commonly used image datasets are inaccessible. Rather than designing metrics for feature spaces with unknown characteristics, we propose to measure GAN performance by evaluating on explicitly parameterized, synthetic data distributions. As a case study, we examine the performance of 16 GAN variants on six multivariate distributions of varying dimensionalities and training set sizes. In this learning environment, we observe that: GANs exhibit similar performance trends across dimensionalities; learning depends on the underlying distribution and its complexity; the number of training samples can have a large impact on performance; evaluation and relative comparisons are metric-dependent; diverse sets of hyperparameters can produce a "best" result; and some GANs are more robust to hyperparameter changes than others. These observations both corroborate findings of previous GAN evaluation studies and make novel contributions regarding the relationship between size, complexity, and GAN performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge