Estimating expectation values using approximate quantum states
Paper and Code
Nov 11, 2020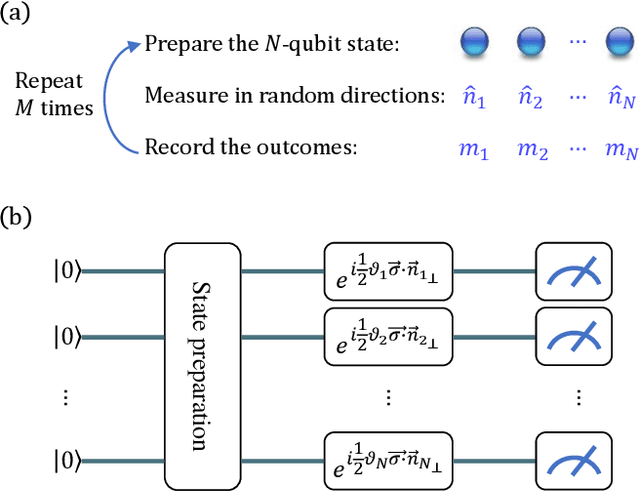
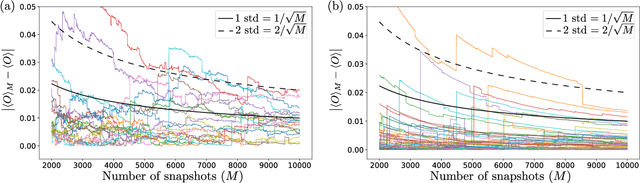
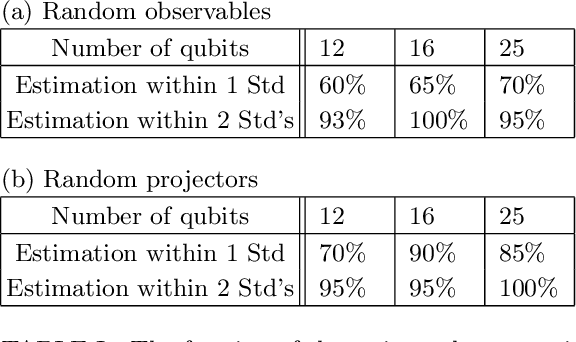
We introduce an approximate description of an $N$-qubit state, which contains sufficient information to estimate the expectation value of any observable to a precision that is upper bounded by the ratio of a suitably-defined seminorm of the observable to the square root of the number of the system's identical preparations $M$, with no explicit dependence on $N$. We describe an operational procedure for constructing the approximate description of the state that requires, besides the quantum state preparation, only single-qubit rotations followed by single-qubit measurements. We show that following this procedure, the cardinality of the resulting description of the state grows as $3MN$. We test the proposed method on Rigetti's quantum processor unit with 12, 16 and 25 qubits for random states and random observables, and find an excellent agreement with the theory, despite experimental errors.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge