Encoding prior knowledge in the structure of the likelihood
Paper and Code
Dec 11, 2018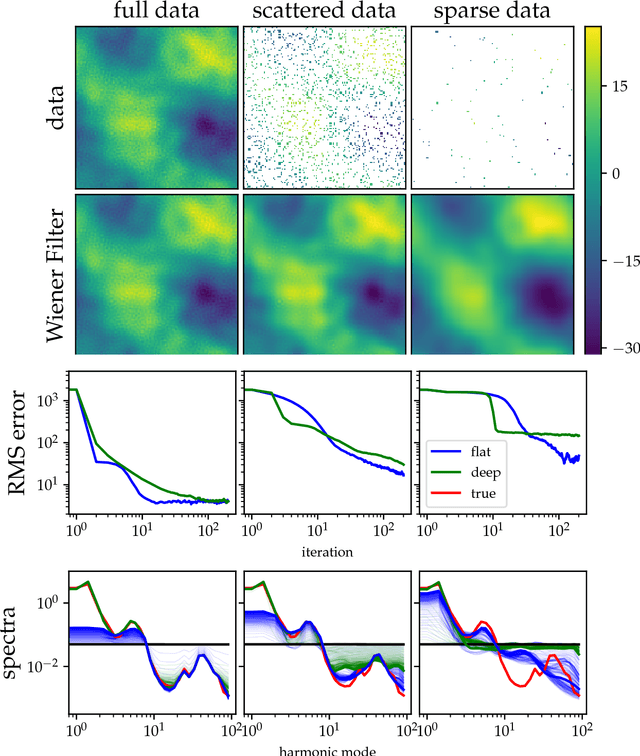
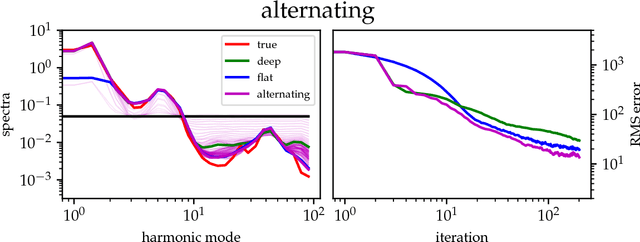
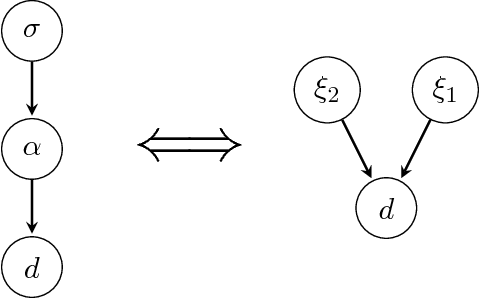
The inference of deep hierarchical models is problematic due to strong dependencies between the hierarchies. We investigate a specific transformation of the model parameters based on the multivariate distributional transform. This transformation is a special form of the reparametrization trick, flattens the hierarchy and leads to a standard Gaussian prior on all resulting parameters. The transformation also transfers all the prior information into the structure of the likelihood, hereby decoupling the transformed parameters a priori from each other. A variational Gaussian approximation in this standardized space will be excellent in situations of relatively uninformative data. Additionally, the curvature of the log-posterior is well-conditioned in directions that are weakly constrained by the data, allowing for fast inference in such a scenario. In an example we perform the transformation explicitly for Gaussian process regression with a priori unknown correlation structure. Deep models are inferred rapidly in highly and slowly in poorly informed situations. The flat model show exactly the opposite performance pattern. A synthesis of both, the deep and the flat perspective, provides their combined advantages and overcomes the individual limitations, leading to a faster inference.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge