EiGLasso for Scalable Sparse Kronecker-Sum Inverse Covariance Estimation
Paper and Code
May 20, 2021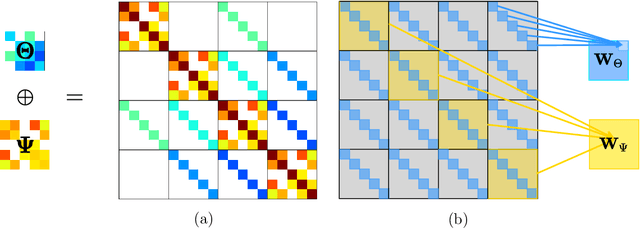
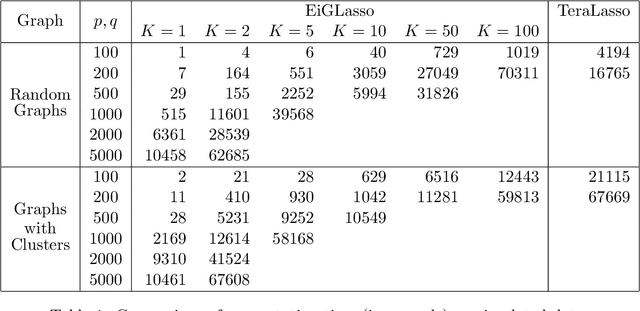

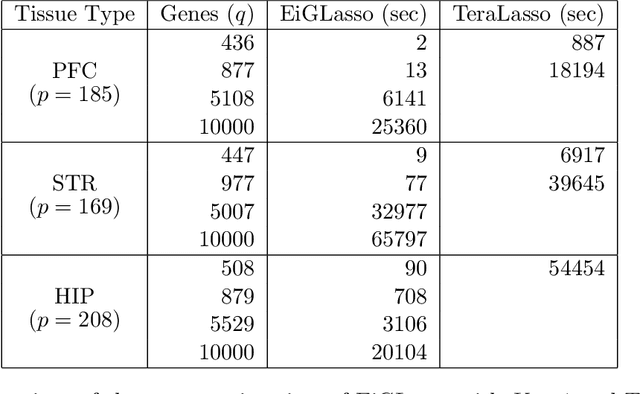
In many real-world problems, complex dependencies are present both among samples and among features. The Kronecker sum or the Cartesian product of two graphs, each modeling dependencies across features and across samples, has been used as an inverse covariance matrix for a matrix-variate Gaussian distribution, as an alternative to a Kronecker-product inverse covariance matrix, due to its more intuitive sparse structure. However, the existing methods for sparse Kronecker-sum inverse covariance estimation are limited in that they do not scale to more than a few hundred features and samples and that the unidentifiable parameters pose challenges in estimation. In this paper, we introduce EiGLasso, a highly scalable method for sparse Kronecker-sum inverse covariance estimation, based on Newton's method combined with eigendecomposition of the two graphs for exploiting the structure of Kronecker sum. EiGLasso further reduces computation time by approximating the Hessian based on the eigendecomposition of the sample and feature graphs. EiGLasso achieves quadratic convergence with the exact Hessian and linear convergence with the approximate Hessian. We describe a simple new approach to estimating the unidentifiable parameters that generalizes the existing methods. On simulated and real-world data, we demonstrate that EiGLasso achieves two to three orders-of-magnitude speed-up compared to the existing methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge