Efficient line search for optimizing Area Under the ROC Curve in gradient descent

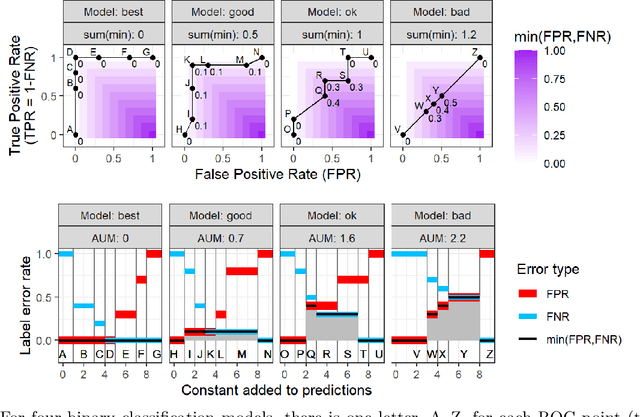
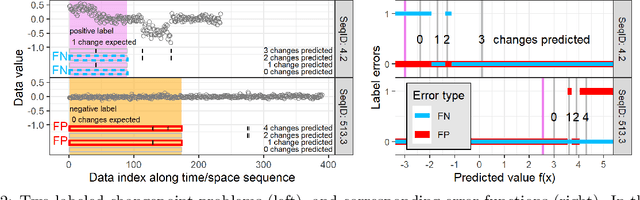
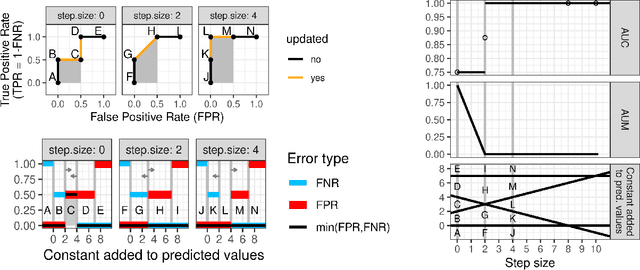
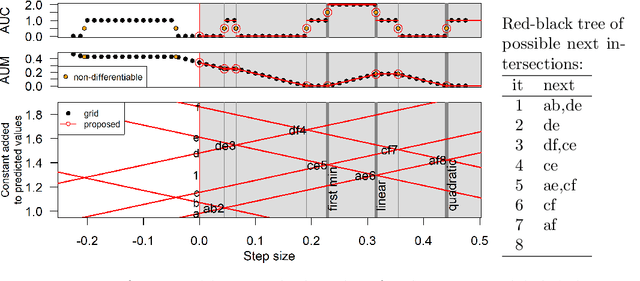
Receiver Operating Characteristic (ROC) curves are useful for evaluation in binary classification and changepoint detection, but difficult to use for learning since the Area Under the Curve (AUC) is piecewise constant (gradient zero almost everywhere). Recently the Area Under Min (AUM) of false positive and false negative rates has been proposed as a differentiable surrogate for AUC. In this paper we study the piecewise linear/constant nature of the AUM/AUC, and propose new efficient path-following algorithms for choosing the learning rate which is optimal for each step of gradient descent (line search), when optimizing a linear model. Remarkably, our proposed line search algorithm has the same log-linear asymptotic time complexity as gradient descent with constant step size, but it computes a complete representation of the AUM/AUC as a function of step size. In our empirical study of binary classification problems, we verify that our proposed algorithm is fast and exact; in changepoint detection problems we show that the proposed algorithm is just as accurate as grid search, but faster.