Efficient 2D neuron boundary segmentation with local topological constraints
Paper and Code
Feb 03, 2020
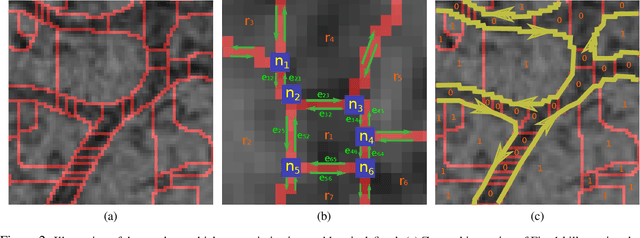
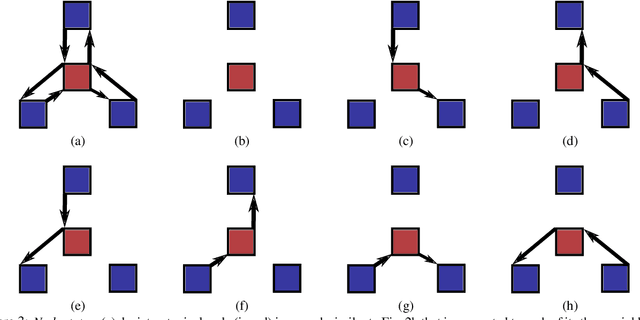
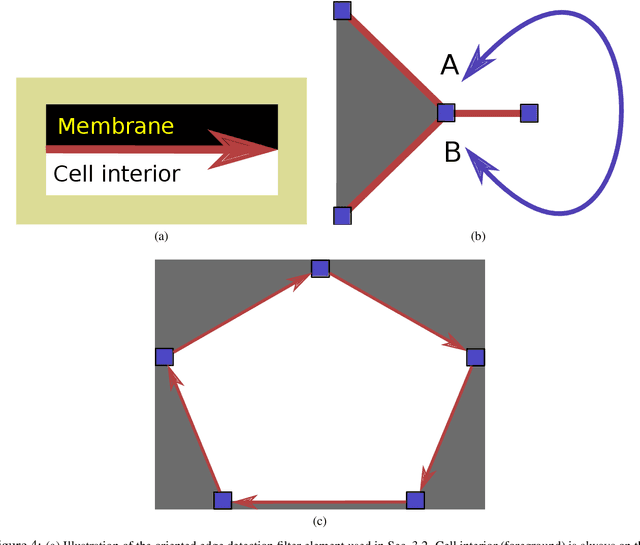
We present a method for segmenting neuron membranes in 2D electron microscopy imagery. This segmentation task has been a bottleneck to reconstruction efforts of the brain's synaptic circuits. One common problem is the misclassification of blurry membrane fragments as cell interior, which leads to merging of two adjacent neuron sections into one via the blurry membrane region. Human annotators can easily avoid such errors by implicitly performing gap completion, taking into account the continuity of membranes. Drawing inspiration from these human strategies, we formulate the segmentation task as an edge labeling problem on a graph with local topological constraints. We derive an integer linear program (ILP) that enforces membrane continuity, i.e. the absence of gaps. The cost function of the ILP is the pixel-wise deviation of the segmentation from a priori membrane probabilities derived from the data. Based on membrane probability maps obtained using random forest classifiers and convolutional neural networks, our method improves the neuron boundary segmentation accuracy compared to a variety of standard segmentation approaches. Our method successfully performs gap completion and leads to fewer topological errors. The method could potentially also be incorporated into other image segmentation pipelines with known topological constraints.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge