Dynamic Multi-objective Ensemble of Acquisition Functions in Batch Bayesian Optimization
Paper and Code
Jun 22, 2022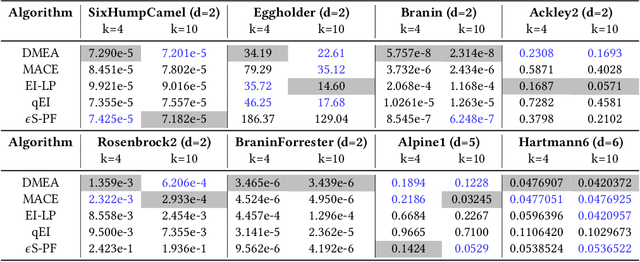
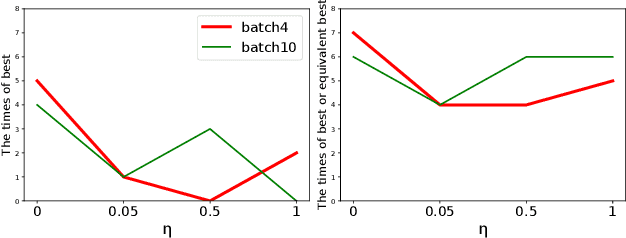
Bayesian optimization (BO) is a typical approach to solve expensive optimization problems. In each iteration of BO, a Gaussian process(GP) model is trained using the previously evaluated solutions; then next candidate solutions for expensive evaluation are recommended by maximizing a cheaply-evaluated acquisition function on the trained surrogate model. The acquisition function plays a crucial role in the optimization process. However, each acquisition function has its own strengths and weaknesses, and no single acquisition function can consistently outperform the others on all kinds of problems. To better leverage the advantages of different acquisition functions, we propose a new method for batch BO. In each iteration, three acquisition functions are dynamically selected from a set based on their current and historical performance to form a multi-objective optimization problem (MOP). Using an evolutionary multi-objective algorithm to optimize such a MOP, a set of non-dominated solutions can be obtained. To select batch candidate solutions, we rank these non-dominated solutions into several layers according to their relative performance on the three acquisition functions. The empirical results show that the proposed method is competitive with the state-of-the-art methods on different problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge