DUAL-LOCO: Distributing Statistical Estimation Using Random Projections
Paper and Code
Jan 08, 2016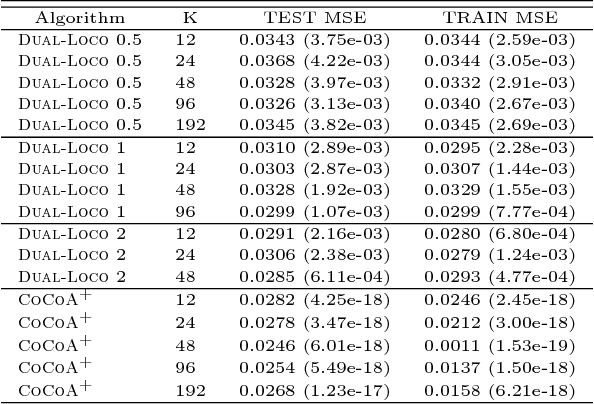
We present DUAL-LOCO, a communication-efficient algorithm for distributed statistical estimation. DUAL-LOCO assumes that the data is distributed according to the features rather than the samples. It requires only a single round of communication where low-dimensional random projections are used to approximate the dependences between features available to different workers. We show that DUAL-LOCO has bounded approximation error which only depends weakly on the number of workers. We compare DUAL-LOCO against a state-of-the-art distributed optimization method on a variety of real world datasets and show that it obtains better speedups while retaining good accuracy.
* Proceedings of the 19th International Conference on Artificial
Intelligence and Statistics, 51, 2016, 12 pages * 13 pages
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge