DPER: Dynamic Programming for Exist-Random Stochastic SAT
Paper and Code
May 19, 2022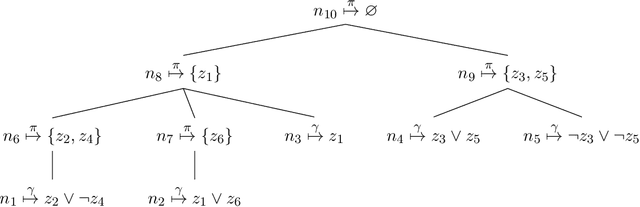
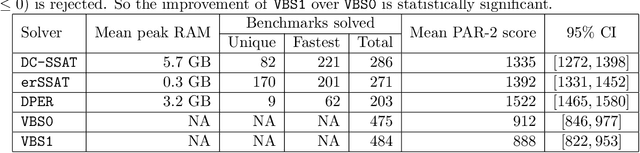
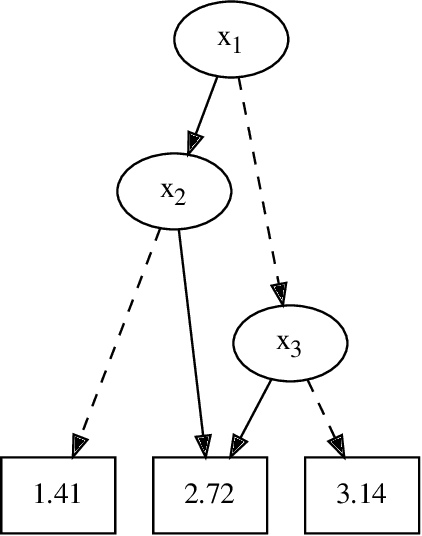
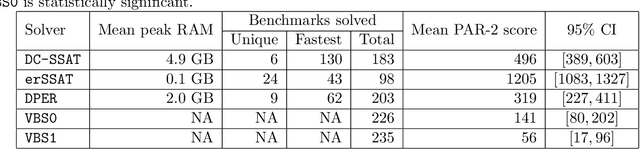
In Bayesian inference, the maximum a posteriori (MAP) problem combines the most probable explanation (MPE) and marginalization (MAR) problems. The counterpart in propositional logic is the exist-random stochastic satisfiability (ER-SSAT) problem, which combines the satisfiability (SAT) and weighted model counting (WMC) problems. Both MAP and ER-SSAT have the form $\operatorname{argmax}_X \sum_Y f(X, Y)$, where $f$ is a real-valued function over disjoint sets $X$ and $Y$ of variables. These two optimization problems request a value assignment for the $X$ variables that maximizes the weighted sum of $f(X, Y)$ over all value assignments for the $Y$ variables. ER-SSAT has been shown to be a promising approach to formally verify fairness in supervised learning. Recently, dynamic programming on graded project-join trees has been proposed to solve weighted projected model counting (WPMC), a related problem that has the form $\sum_X \max_Y f(X, Y)$. We extend this WPMC framework to exactly solve ER-SSAT and implement a dynamic-programming solver named DPER. Our empirical evaluation indicates that DPER contributes to the portfolio of state-of-the-art ER-SSAT solvers (DC-SSAT and erSSAT) through competitive performance on low-width problem instances.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge