Downlink SCMA Codebook Design with Low Error Rate by Maximizing Minimum Euclidean Distance of Superimposed Codewords

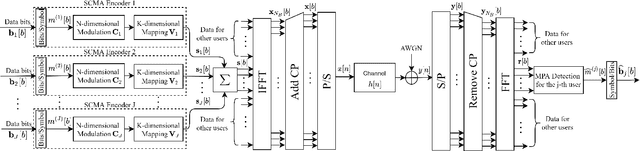
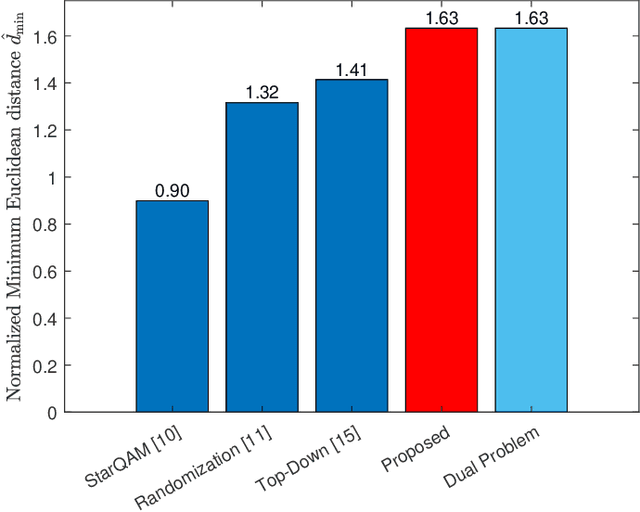
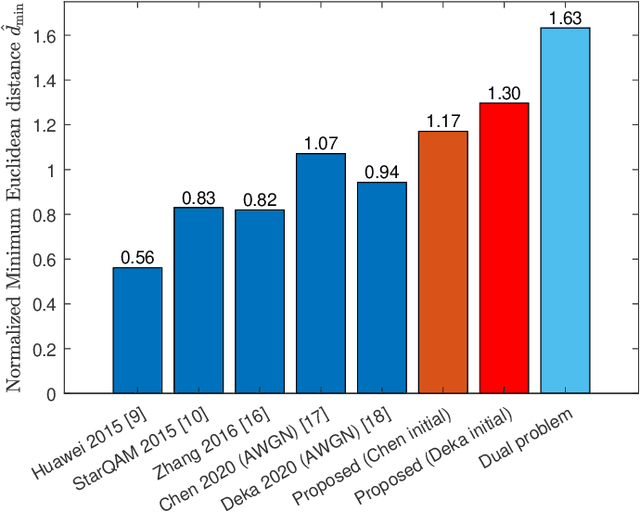
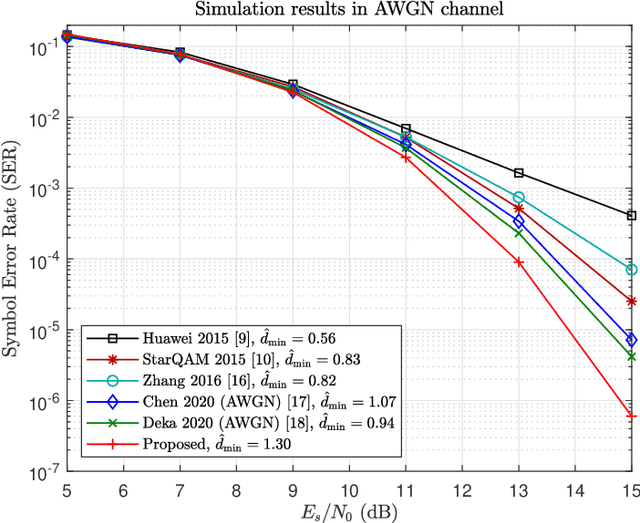
Sparse code multiple access (SCMA), as a codebook-based non-orthogonal multiple access (NOMA) technique, has received research attention in recent years. The codebook design problem for SCMA has also been studied to some extent since codebook choices are highly related to the system's error rate performance. In this paper, we approach the downlink SCMA codebook design problem by formulating an optimization problem to maximize the minimum Euclidean distance (MED) of superimposed codewords under power constraints. While SCMA codebooks with a larger minimum Euclidean distance (MED) are expected to obtain a better BER performance, no optimal SCMA codebook in terms of MED maximization, to the authors' best knowledge, has been reported in the SCMA literature yet. In this paper, a new iterative algorithm based on alternating maximization with exact penalty is proposed for the MED maximization problem. The proposed algorithm, when supplied with appropriate initial points and parameters, achieves a set of codebooks of all users whose MED is larger than any previously reported results. A Lagrange dual problem is derived which provides an upper bound of MED of any set of codebooks. Even though there is still a nonzero gap between the achieved MED and the upper bound given by the dual problem, simulation results demonstrate clear advantages in error rate performances of the proposed set of codebooks over all existing ones. The correctness and accuracy of error curves in the simulation results are further confirmed by the coincidences with the theoretical upper bounds of error rates derived for any given set of codebooks.