Discrete MMSE Precoding for Multiuser MIMO Systems with PSK Modulation
Paper and Code
May 24, 2021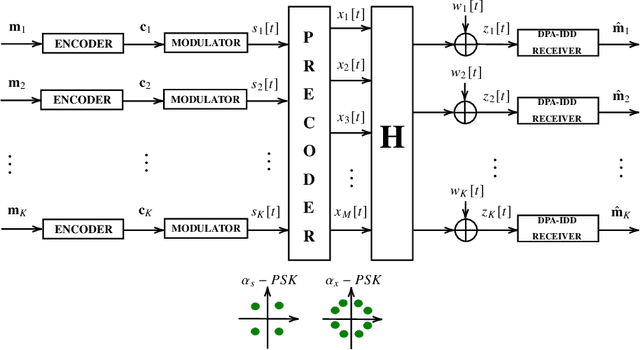
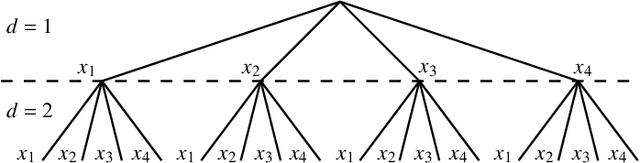
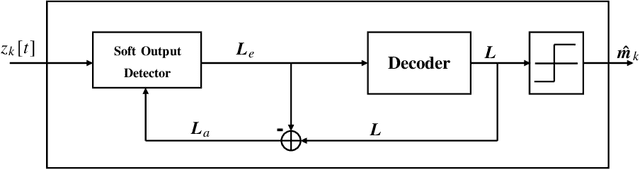
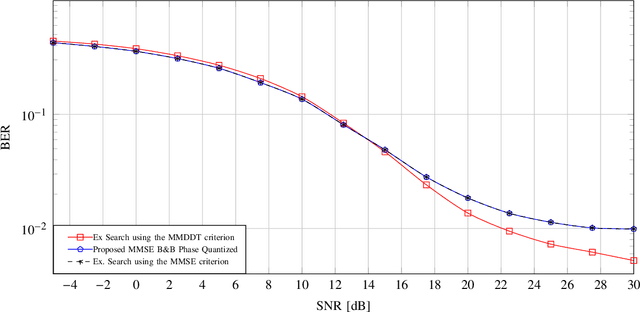
We propose an optimal MMSE precoding technique using quantized signals with constant envelope. Unlike the existing MMSE design that relies on 1-bit resolution, the proposed approach employs uniform phase quantization and the bounding step in the branch-and-bound method is different in terms of considering the most restrictive relaxation of the nonconvex problem, which is then utilized for a suboptimal design also. Moreover, unlike prior studies, we propose three different soft detection methods and an iterative detection and decoding scheme that allow the utilization of channel coding in conjunction with low-resolution precoding. Besides an exact approach for computing the extrinsic information, we propose two approximations with reduced computational complexity. Numerical simulations show that utilizing the MMSE criterion instead of the established maximum-minimum distance to the decision threshold yields a lower bit-error-rate in many scenarios. Furthermore, when using the MMSE criterion, a smaller number of bound evaluations in the branch-and-bound method is required for low and medium SNR. Finally, results based on an LDPC block code indicate that the receive processing schemes yield a lower bit-error-rate compared to the conventional design.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge