Deterministic Bayesian Information Fusion and the Analysis of its Performance
Paper and Code
Nov 02, 2014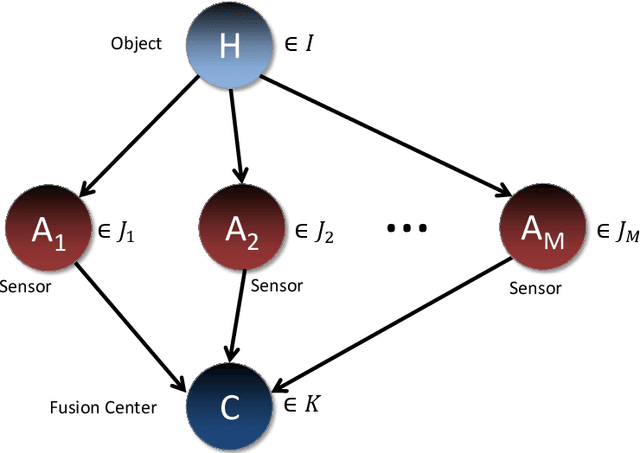
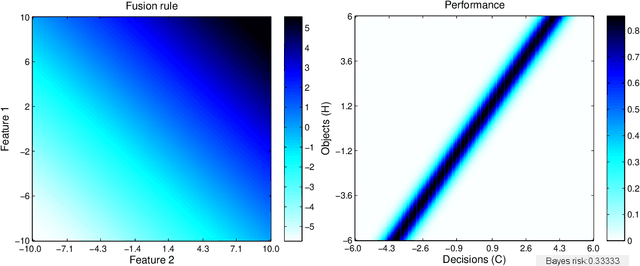
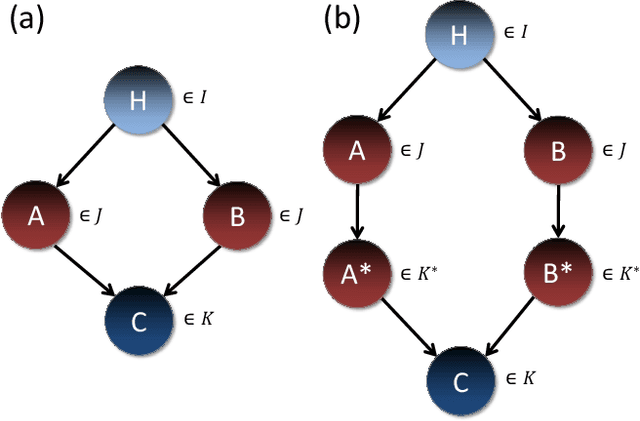
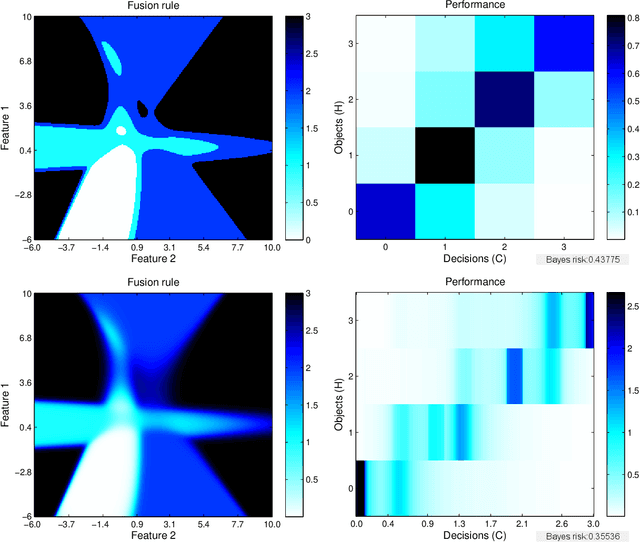
This paper develops a mathematical and computational framework for analyzing the expected performance of Bayesian data fusion, or joint statistical inference, within a sensor network. We use variational techniques to obtain the posterior expectation as the optimal fusion rule under a deterministic constraint and a quadratic cost, and study the smoothness and other properties of its classification performance. For a certain class of fusion problems, we prove that this fusion rule is also optimal in a much wider sense and satisfies strong asymptotic convergence results. We show how these results apply to a variety of examples with Gaussian, exponential and other statistics, and discuss computational methods for determining the fusion system's performance in more general, large-scale problems. These results are motivated by studying the performance of fusing multi-modal radar and acoustic sensors for detecting explosive substances, but have broad applicability to other Bayesian decision problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge