Determining the Number of Clusters via Iterative Consensus Clustering
Paper and Code
Aug 05, 2014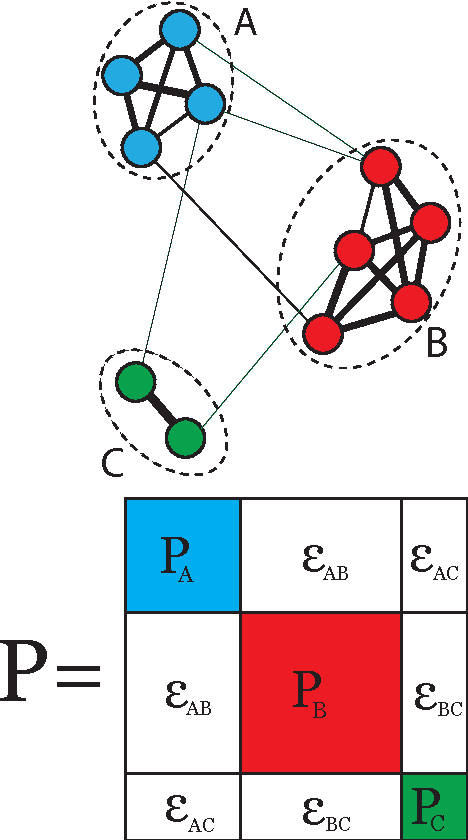

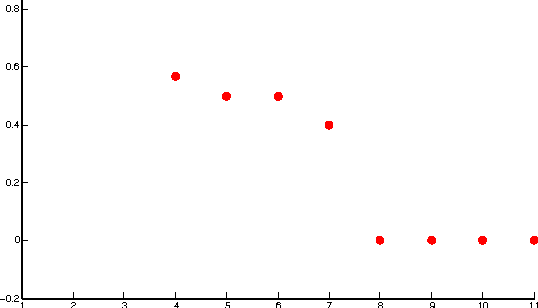

We use a cluster ensemble to determine the number of clusters, k, in a group of data. A consensus similarity matrix is formed from the ensemble using multiple algorithms and several values for k. A random walk is induced on the graph defined by the consensus matrix and the eigenvalues of the associated transition probability matrix are used to determine the number of clusters. For noisy or high-dimensional data, an iterative technique is presented to refine this consensus matrix in way that encourages a block-diagonal form. It is shown that the resulting consensus matrix is generally superior to existing similarity matrices for this type of spectral analysis.
* Proceedings of the 2013 SIAM International Conference on Data Mining
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge