Detecting Hidden Triggers: Mapping Non-Markov Reward Functions to Markov
Paper and Code
Jan 20, 2024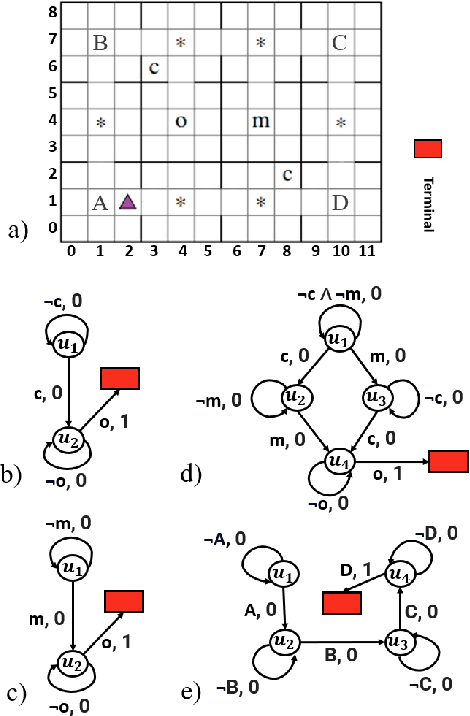

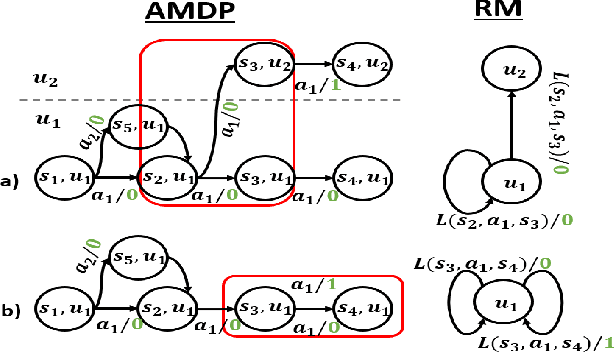
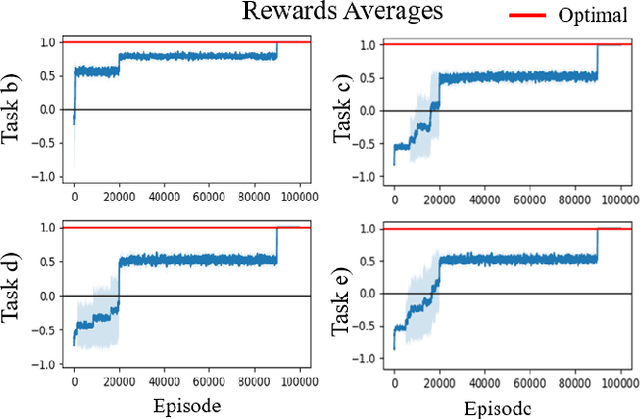
Many Reinforcement Learning algorithms assume a Markov reward function to guarantee optimality. However, not all reward functions are known to be Markov. In this paper, we propose a framework for mapping non-Markov reward functions into equivalent Markov ones by learning a Reward Machine - a specialized reward automaton. Unlike the general practice of learning Reward Machines, we do not require a set of high-level propositional symbols from which to learn. Rather, we learn \emph{hidden triggers} directly from data that encode them. We demonstrate the importance of learning Reward Machines versus their Deterministic Finite-State Automata counterparts, for this task, given their ability to model reward dependencies in a single automaton. We formalize this distinction in our learning objective. Our mapping process is constructed as an Integer Linear Programming problem. We prove that our mappings provide consistent expectations for the underlying process. We empirically validate our approach by learning black-box non-Markov Reward functions in the Officeworld Domain. Additionally, we demonstrate the effectiveness of learning dependencies between rewards in a new domain, Breakfastworld.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge