Deep neural networks architectures from the perspective of manifold learning
Paper and Code
Jun 06, 2023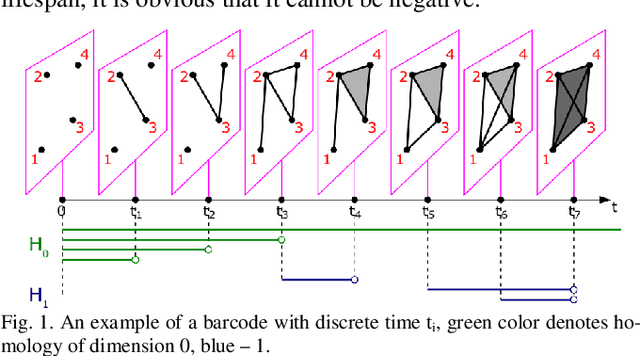
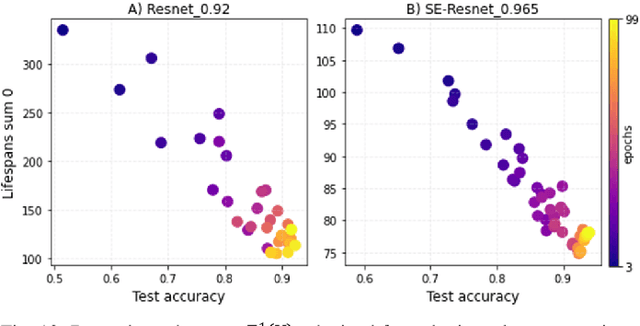
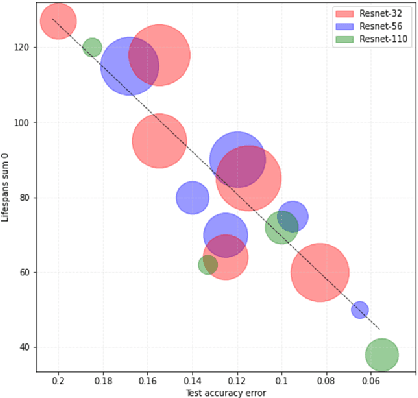
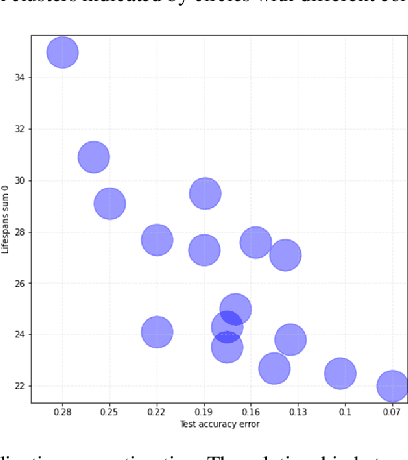
Despite significant advances in the field of deep learning in ap-plications to various areas, an explanation of the learning pro-cess of neural network models remains an important open ques-tion. The purpose of this paper is a comprehensive comparison and description of neural network architectures in terms of ge-ometry and topology. We focus on the internal representation of neural networks and on the dynamics of changes in the topology and geometry of a data manifold on different layers. In this paper, we use the concepts of topological data analysis (TDA) and persistent homological fractal dimension. We present a wide range of experiments with various datasets and configurations of convolutional neural network (CNNs) architectures and Transformers in CV and NLP tasks. Our work is a contribution to the development of the important field of explainable and interpretable AI within the framework of geometrical deep learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge