Deep Linear Networks can Benignly Overfit when Shallow Ones Do
Paper and Code
Sep 19, 2022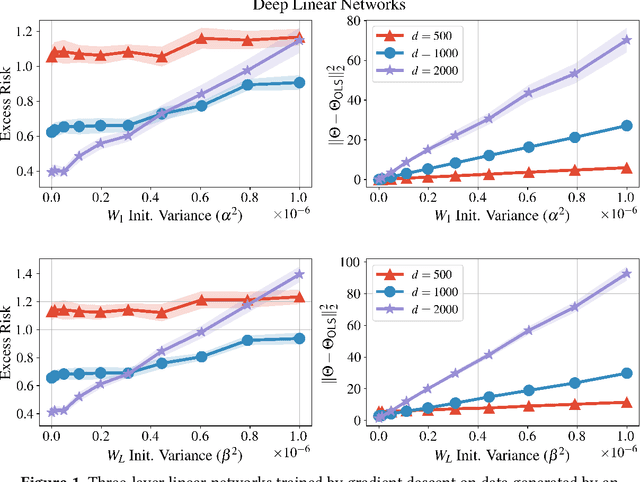
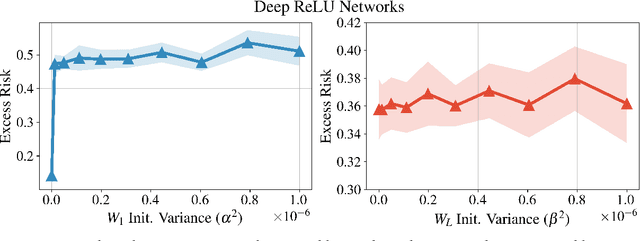

We bound the excess risk of interpolating deep linear networks trained using gradient flow. In a setting previously used to establish risk bounds for the minimum $\ell_2$-norm interpolant, we show that randomly initialized deep linear networks can closely approximate or even match known bounds for the minimum $\ell_2$-norm interpolant. Our analysis also reveals that interpolating deep linear models have exactly the same conditional variance as the minimum $\ell_2$-norm solution. Since the noise affects the excess risk only through the conditional variance, this implies that depth does not improve the algorithm's ability to "hide the noise". Our simulations verify that aspects of our bounds reflect typical behavior for simple data distributions. We also find that similar phenomena are seen in simulations with ReLU networks, although the situation there is more nuanced.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge