Deep Fréchet Regression
Paper and Code
Jul 31, 2024
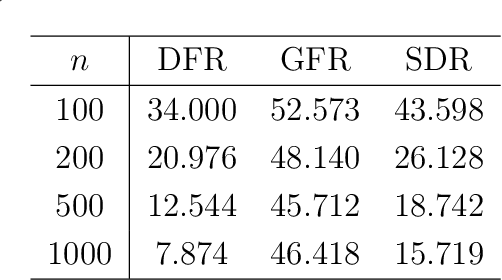
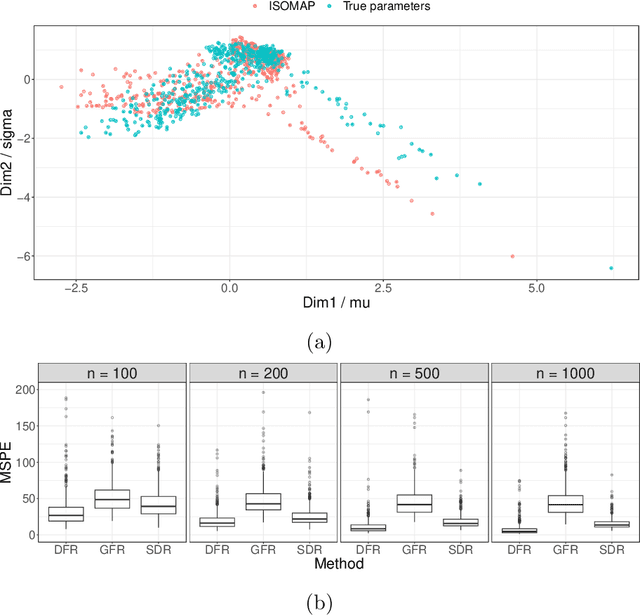
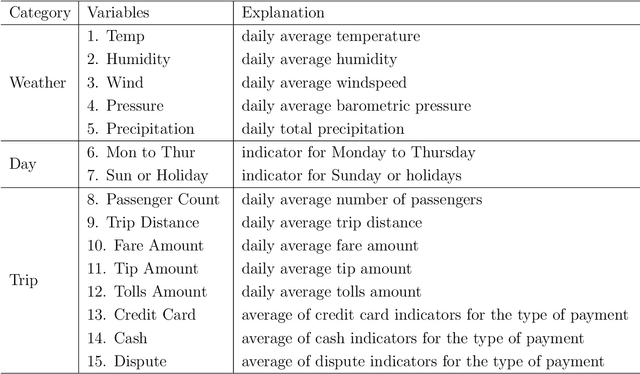
Advancements in modern science have led to the increasing availability of non-Euclidean data in metric spaces. This paper addresses the challenge of modeling relationships between non-Euclidean responses and multivariate Euclidean predictors. We propose a flexible regression model capable of handling high-dimensional predictors without imposing parametric assumptions. Two primary challenges are addressed: the curse of dimensionality in nonparametric regression and the absence of linear structure in general metric spaces. The former is tackled using deep neural networks, while for the latter we demonstrate the feasibility of mapping the metric space where responses reside to a low-dimensional Euclidean space using manifold learning. We introduce a reverse mapping approach, employing local Fr\'echet regression, to map the low-dimensional manifold representations back to objects in the original metric space. We develop a theoretical framework, investigating the convergence rate of deep neural networks under dependent sub-Gaussian noise with bias. The convergence rate of the proposed regression model is then obtained by expanding the scope of local Fr\'echet regression to accommodate multivariate predictors in the presence of errors in predictors. Simulations and case studies show that the proposed model outperforms existing methods for non-Euclidean responses, focusing on the special cases of probability measures and networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge