Data ultrametricity and clusterability
Paper and Code
Aug 28, 2019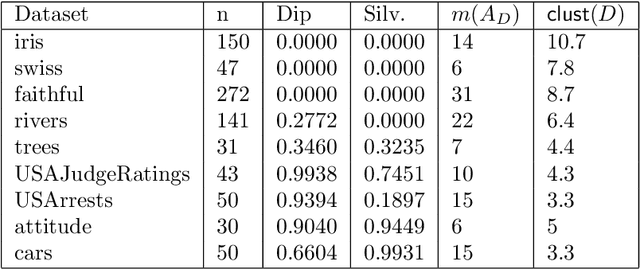
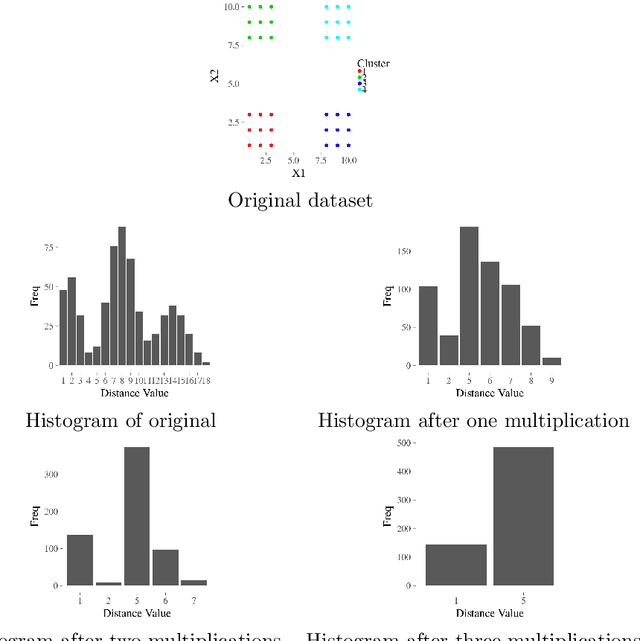
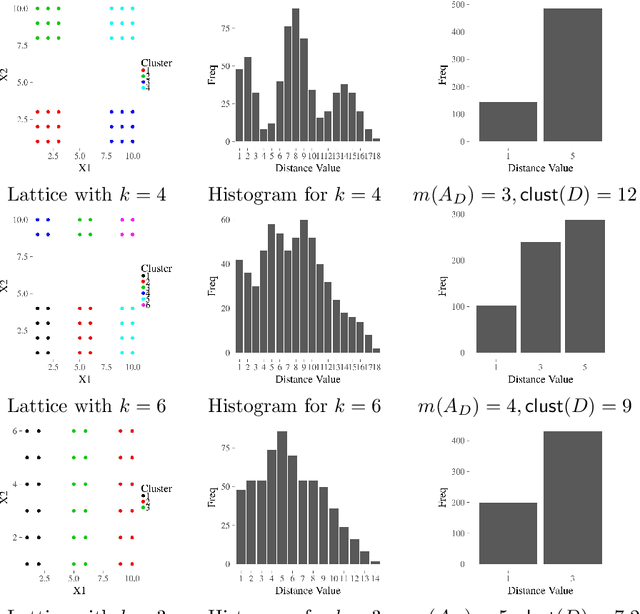
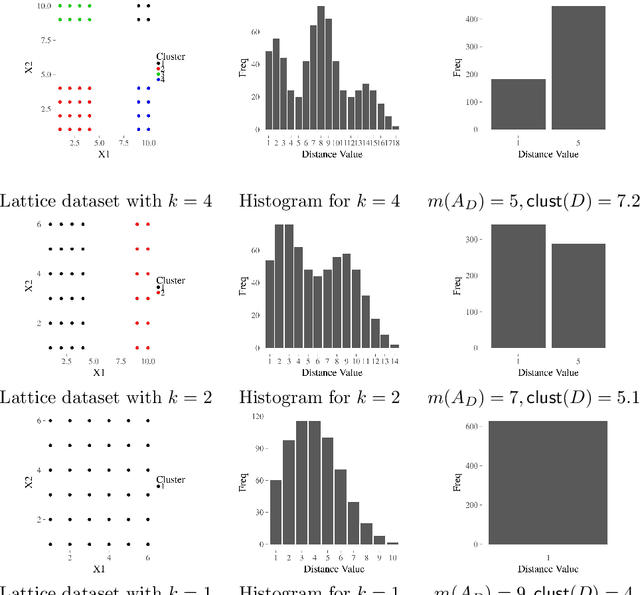
The increasing needs of clustering massive datasets and the high cost of running clustering algorithms poses difficult problems for users. In this context it is important to determine if a data set is clusterable, that is, it may be partitioned efficiently into well-differentiated groups containing similar objects. We approach data clusterability from an ultrametric-based perspective. A novel approach to determine the ultrametricity of a dataset is proposed via a special type of matrix product, which allows us to evaluate the clusterability of the dataset. Furthermore, we show that by applying our technique to a dissimilarity space will generate the sub-dominant ultrametric of the dissimilarity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge