Data-driven rogue waves and parameter discovery in the defocusing NLS equation with a potential using the PINN deep learning
Paper and Code
Dec 18, 2020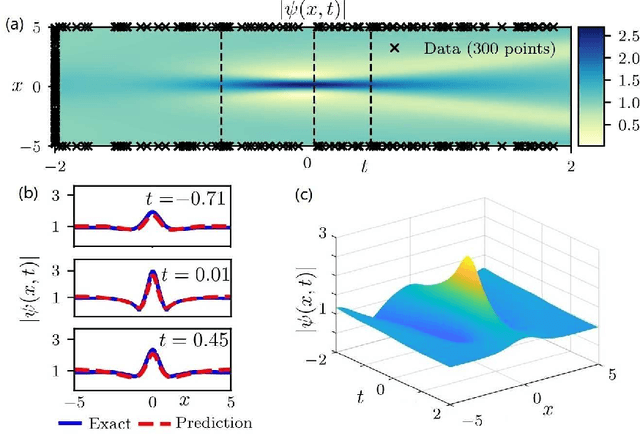
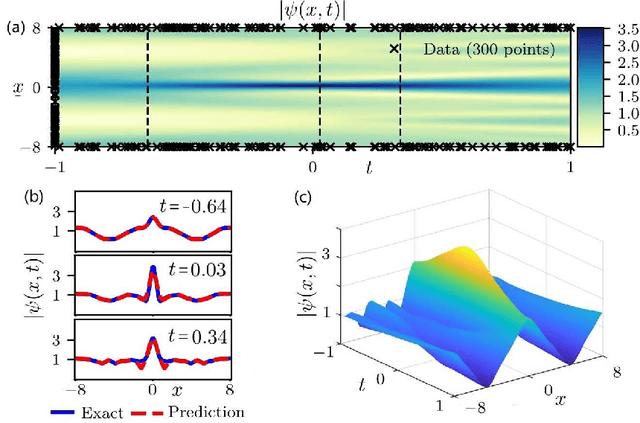
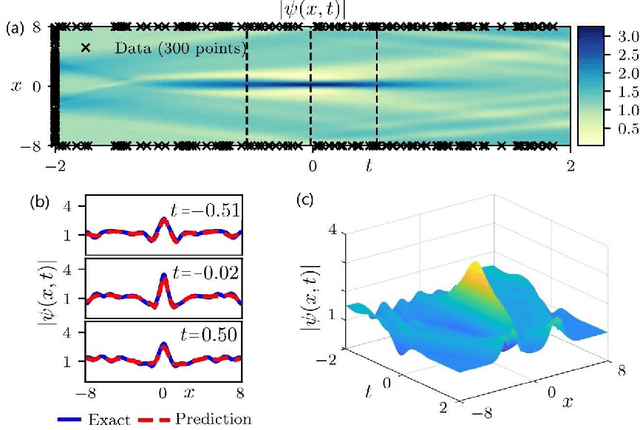
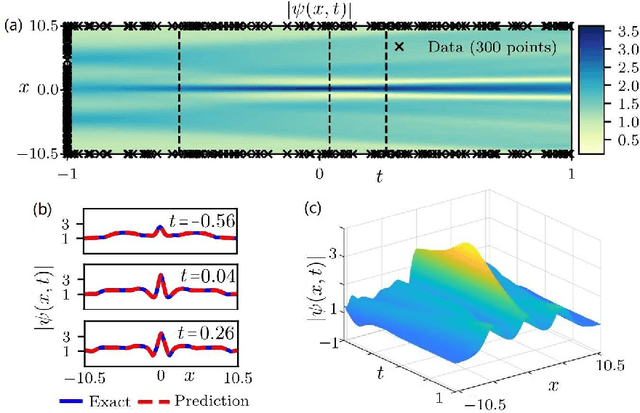
The physics-informed neural networks (PINNs) can be used to deep learn the nonlinear partial differential equations and other types of physical models. In this paper, we use the multi-layer PINN deep learning method to study the data-driven rogue wave solutions of the defocusing nonlinear Schr\"odinger (NLS) equation with the time-dependent potential by considering several initial conditions such as the rogue wave, Jacobi elliptic cosine function, two-Gaussian function, or three-hyperbolic-secant function, and periodic boundary conditions. Moreover, the multi-layer PINN algorithm can also be used to learn the parameter in the defocusing NLS equation with the time-dependent potential under the sense of the rogue wave solution. These results will be useful to further discuss the rogue wave solutions of the defocusing NLS equation with a potential in the study of deep learning neural networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge