Data-driven peakon and periodic peakon travelling wave solutions of some nonlinear dispersive equations via deep learning
Paper and Code
Jan 12, 2021
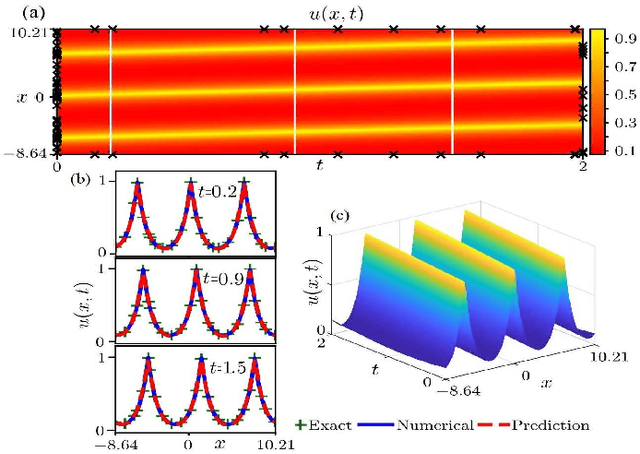
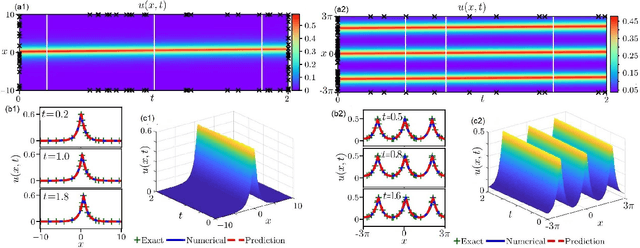
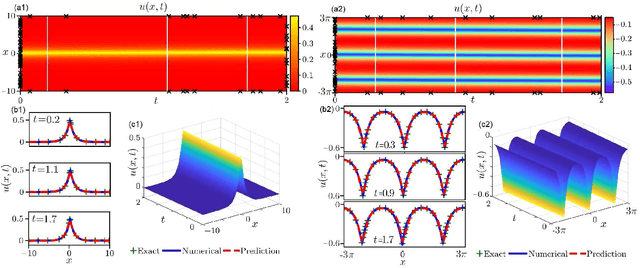
In the field of mathematical physics, there exist many physically interesting nonlinear dispersive equations with peakon solutions, which are solitary waves with discontinuous first-order derivative at the wave peak. In this paper, we apply the multi-layer physics-informed neural networks (PINNs) deep learning to successfully study the data-driven peakon and periodic peakon solutions of some well-known nonlinear dispersion equations with initial-boundary value conditions such as the Camassa-Holm (CH) equation, Degasperis-Procesi equation, modified CH equation with cubic nonlinearity, Novikov equation with cubic nonlinearity, mCH-Novikov equation, b-family equation with quartic nonlinearity, generalized modified CH equation with quintic nonlinearity, and etc. These results will be useful to further study the peakon solutions and corresponding experimental design of nonlinear dispersive equations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge