Data-driven low-dimensional model of a sedimenting flexible fiber
Paper and Code
May 16, 2024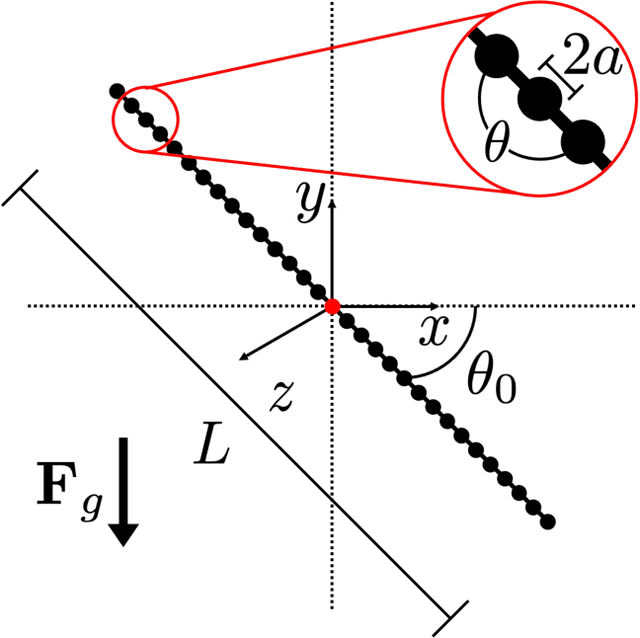
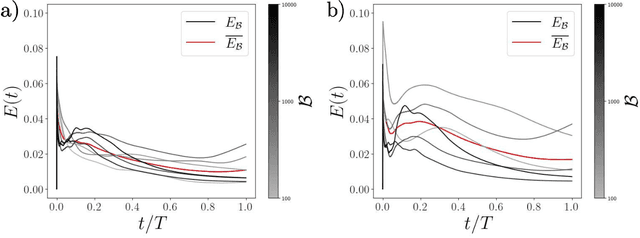
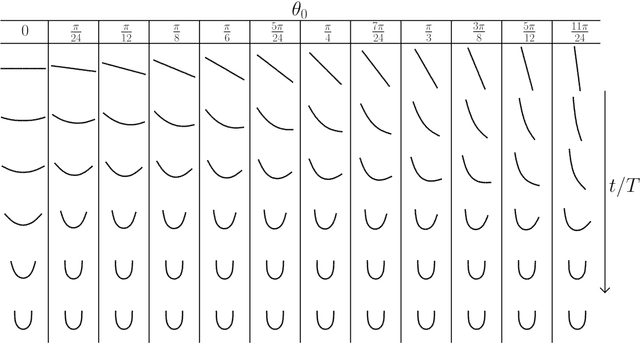
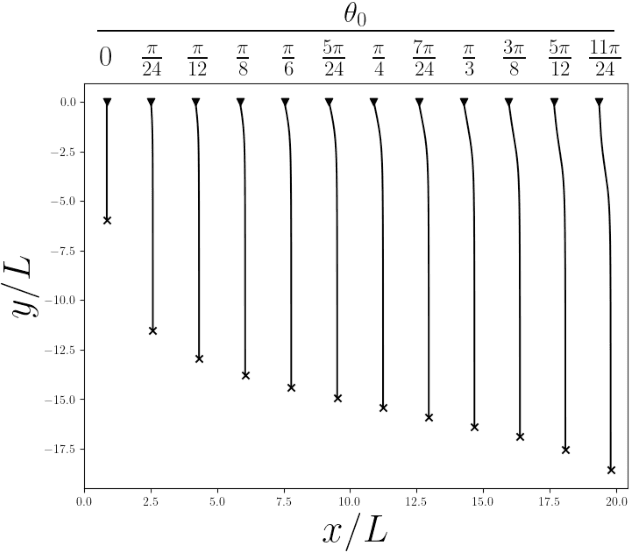
The dynamics of flexible filaments entrained in flow, important for understanding many biological and industrial processes, are computationally expensive to model with full-physics simulations. This work describes a data-driven technique to create high-fidelity low-dimensional models of flexible fiber dynamics using machine learning; the technique is applied to sedimentation in a quiescent, viscous Newtonian fluid, using results from detailed simulations as the data set. The approach combines an autoencoder neural network architecture to learn a low-dimensional latent representation of the filament shape, with a neural ODE that learns the evolution of the particle in the latent state. The model was designed to model filaments of varying flexibility, characterized by an elasto-gravitational number $\mathcal{B}$, and was trained on a data set containing the evolution of fibers beginning at set angles of inclination. For the range of $\mathcal{B}$ considered here (100-10000), the filament shape dynamics can be represented with high accuracy with only four degrees of freedom, in contrast to the 93 present in the original bead-spring model used to generate the dynamic trajectories. We predict the evolution of fibers set at arbitrary angles and demonstrate that our data-driven model can accurately forecast the evolution of a fiber at both trained and untrained elasto-gravitational numbers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge